
| 喜欢街舞 | 不喜欢街舞 | 合计 | |
| 男生 | 184 | 26 | 210 |
| 女生 | 200 | 50 | 250 |
| 合计 | 384 | 76 | 460 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 90 | B. | 95 | C. | 97.5 | D. | 99 |
 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∉R,tanx≠1 | B. | ?x∈R,tanx=1 | C. | ?x0∉Rtanx0=1 | D. | ?x0∈R,tanx0=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥l,n⊥l,则m∥n | B. | 若l∥m,l?α,则α∥β | ||
| C. | 若m∥l,m∥α,则l∥α | D. | 若α⊥γ,β⊥γ,α∩β=l,则l⊥γ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin2x | B. | y=|cosx| | C. | y=-tanx | D. | $y=cos\frac{x}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
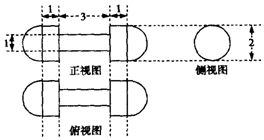 某几何体由三个圆柱和大小相同的两个半球组成,它的三视图如图所示(单位:dm),则该几何体的表面积是( )(侧视图中间有小圆)
某几何体由三个圆柱和大小相同的两个半球组成,它的三视图如图所示(单位:dm),则该几何体的表面积是( )(侧视图中间有小圆)| A. | $\frac{25π}{2}$dm2 | B. | 11πdm2 | C. | $\frac{19π}{2}$dm2 | D. | 9πdm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
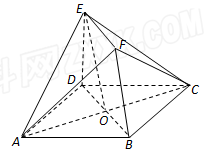 如图,正方形ABCD和直角梯形BDEF所在的平面互相垂直,O为正方形ABCD的中心,AD=DE=2$\sqrt{2}$,EF∥BD,BD=2EF,DE⊥BD.
如图,正方形ABCD和直角梯形BDEF所在的平面互相垂直,O为正方形ABCD的中心,AD=DE=2$\sqrt{2}$,EF∥BD,BD=2EF,DE⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com