
| A. | $\frac{28}{3}$ | B. | $\frac{128}{9}$ | C. | $\frac{128}{8}\sqrt{3}$ | D. | $\frac{28}{3}\sqrt{2}$ |
分析 先设出A,B的坐标,根据抛物线方程求得焦点坐标,利用直线方程的点斜式,求得直线的方程与抛物线方程联立,求得x1=3,x2=$\frac{1}{3}$,然后根据抛物线的定义,答案可得.
解答 解:设A(x1,y1),B(x2,y2)
抛物线的焦点为(1,0),则直线方程为y=$\sqrt{3}$(x-1),
代入抛物线方程得3x2-10x+3=0
∴x1=3,x2=$\frac{1}{3}$,
根据抛物线的定义可知||FA|2-|FB|2|=|(3+$\frac{1}{3}$+2)(3-$\frac{1}{3}$)|=$\frac{128}{9}$,
故选B.
点评 本题主要考查了直线与圆锥曲线的关系,抛物线的简单性质.对学生基础知识的综合考查.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
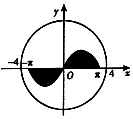 如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点A,则点A落在区域M外的概率是1-$\frac{1}{4π}$.
如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点A,则点A落在区域M外的概率是1-$\frac{1}{4π}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨(¬q) | B. | p∧q | C. | (¬p)∨q | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 6 | C. | 18 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com