
在平面直角坐标系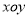 中,已知曲线
中,已知曲线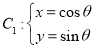 (θ为参数),将
(θ为参数),将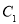 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的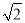 和2倍后得到曲线
和2倍后得到曲线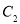 ,以平面直角坐标系
,以平面直角坐标系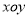 的原点
的原点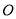 为极点,
为极点,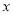 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线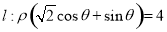 .
.
(1)试写出曲线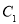 的极坐标方程与曲线
的极坐标方程与曲线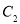 的参数方程;
的参数方程;
(2)在曲线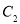 上求一点
上求一点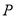 ,使点
,使点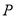 到直线
到直线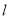 的距离最小,并求此最小值.
的距离最小,并求此最小值.
科目:高中数学 来源:2016届湖南省六校高三12月联考文科数学卷(解析版) 题型:解答题
已知直线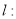
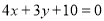 ,半径为
,半径为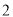 的圆
的圆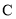 与
与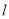 相切,圆心
相切,圆心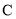 在
在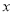 轴上且在直线
轴上且在直线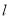 的右上方.
的右上方.
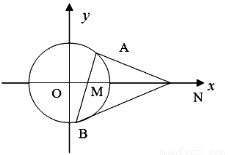
(1)求圆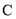 的方程;
的方程;
(2)过点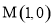 的直线与圆
的直线与圆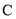 交于
交于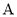 ,
,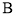 两点(
两点(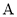 在
在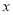 轴上方),问在
轴上方),问在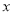 轴正半轴上是否存在定点
轴正半轴上是否存在定点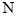 ,使得
,使得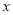 轴平分
轴平分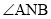 ?若存在,请求出点
?若存在,请求出点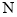 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2016届湖南省六校高三12月联考理科数学卷(解析版) 题型:解答题
株洲市某中学利用周末组织教职员工进行了一次秋季登石峰山健身的活动,有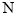 人参加,现将所有参加人员按年龄情况分为
人参加,现将所有参加人员按年龄情况分为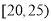 ,
,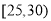 ,
,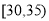 ,
,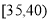 ,
,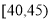 ,
,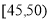 ,
, 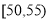 等七组,其频率分布直方图如下图所示.已知
等七组,其频率分布直方图如下图所示.已知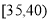 之间的参加者有8人.
之间的参加者有8人.
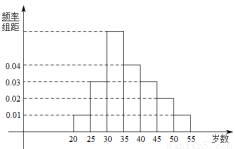
(1)求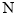 和
和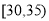 之间的参加者人数
之间的参加者人数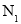 ;
;
(2)已知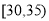 和
和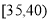 之间各有
之间各有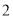 名数学教师,现从这两个组中各选取
名数学教师,现从这两个组中各选取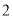 人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有
人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有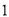 名数学教师的概率?
名数学教师的概率?
(3)组织者从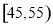 之间的参加者(其中共有
之间的参加者(其中共有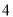 名女教师,其余全为男教师)中随机选取
名女教师,其余全为男教师)中随机选取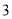 名担任后勤保障工作,其中女教师的人数为
名担任后勤保障工作,其中女教师的人数为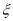 ,求
,求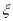 的分布列和数学期望
的分布列和数学期望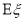 .
.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年浙江慈溪中学高一7-12班上期中数学卷(解析版) 题型:选择题
在直角坐标系中, 如果两点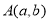 ,
, 在函数
在函数 的图象上,那么称
的图象上,那么称 为函数
为函数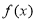 的一组关于原点的中心对称点(
的一组关于原点的中心对称点( 与
与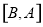 看作一组),函数
看作一组),函数 关于原点的中心对称点的组数为( )
关于原点的中心对称点的组数为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2016届浙江省富阳市高三上学期第二次质量检测理科数学试卷(解析版) 题型:解答题
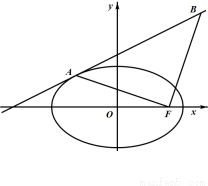
如图所示,椭圆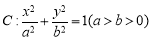 与直线
与直线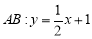 相切于点
相切于点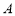 .
.
(1)求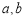 满足的关系式,并用
满足的关系式,并用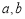 表示点
表示点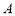 的坐标;
的坐标;
(2)设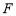 是椭圆的右焦点,若
是椭圆的右焦点,若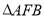 是以
是以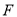 为直角顶点的等腰直角三角形,求椭圆
为直角顶点的等腰直角三角形,求椭圆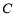 的标准方程.
的标准方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com