解答:
解:(Ⅰ) f'(x)=ae
x(x+2),g'(x)=2x+b----------------------(1分)
由题意,两函数在x=0处有相同的切线.
∴f'(0)=2a,g'(0)=b,
∴2a=b,f(0)=a=g(0)=2,∴a=2,b=4,
∴f(x)=2e
x(x+1),g(x)=x
2+4x+2.----------------------(3分)
(Ⅱ) f'(x)=2e
x(x+2),由f'(x)>0得x>-2,由f'(x)<0得x<-2,
∴f(x)在(-2,+∞)单调递增,在(-∞,-2)单调递减.----------------------(4分)
∵t>-3,∴t+1>-2
①当-3<t<-2时,f(x)在[t,-2]单调递减,[-2,t+1]单调递增,
∴
f(x)min=f(-2)=-2e-2.----------------------(5分)
②当t≥-2时,f(x)在[t,t+1]单调递增,∴
f(x)min=f(t)=2et(t+1);
∴
f(x)=&2et(t+1) (t≥-2)----------------------(6分)
(Ⅲ)令F(x)=kf(x)-g(x)=2ke
x(x+1)-x
2-4x-2,
由题意当x≥-2,F(x)
min≥0----------------------(7分)
∵?x≥-2,kf(x)≥g(x)恒成立,∴F(0)=2k-2≥0,∴k≥1----------------------(8分)
F'(x)=2ke
x(x+1)+2ke
x-2x-4=2(x+2)(ke
x-1),----------------------(9分)
∵x≥-2,由F'(x)>0得
ex>,∴
x>ln;由F'(x)<0得
x<ln∴F(x)在
(-∞,ln]单调递减,在
[ln,+∞)单调递增----------------------(10分)
①当
ln<-2,即k>e
2时,F(x)在[-2,+∞)单调递增,
F(x)min=F(-2)=-2ke-2+2=(e2-k)<0,不满足F(x)
min≥0.----------------(11分)
②当
ln=-2,即k=e
2时,由①知,
F(x)min=F(-2)=(e2-k)=0,满足F(x)
min≥0.-------(12分)
③当
ln>-2,即1≤k<e
2时,F(x)在
[-2,ln]单调递减,在
[ln,+∞)单调递增
F(x)min=F(ln)=lnk(2-lnk)>0,满足F(x)
min≥0.
综上所述,满足题意的k的取值范围为[1,e
2].----------------------(13分)



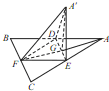 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:


