
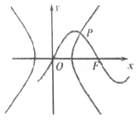
 ��ͼ��ʾ����֪����y=$\sqrt{2}$sin$\frac{��}{4}$x����˫����$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1��a��0��b��0�����ҽ���F������y=$\sqrt{2}$sin$\frac{��}{4}$x��˫�����ڵ�һ������ΪP��P�ĺ�����Ϊ3����˫���ߵĽ����߷���Ϊ��������
��ͼ��ʾ����֪����y=$\sqrt{2}$sin$\frac{��}{4}$x����˫����$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1��a��0��b��0�����ҽ���F������y=$\sqrt{2}$sin$\frac{��}{4}$x��˫�����ڵ�һ������ΪP��P�ĺ�����Ϊ3����˫���ߵĽ����߷���Ϊ��������| A�� | x��y=0 | B�� | x��2y=0 | C�� | x��$\sqrt{3}$y=0 | D�� | 2x��y=0 |
���� �����⣬F��4��0����P��3��1������$\left\{\begin{array}{l}{\frac{9}{{a}^{2}}-\frac{1}{{b}^{2}}=1}\\{{a}^{2}+{b}^{2}=16}\end{array}\right.$�����a��b���������˫���ߵĽ����߷��̣�
��� �⣺�����⣬F��4��0����P��3��1����
��$\left\{\begin{array}{l}{\frac{9}{{a}^{2}}-\frac{1}{{b}^{2}}=1}\\{{a}^{2}+{b}^{2}=16}\end{array}\right.$����a=b=2$\sqrt{2}$��
��˫���ߵĽ����߷���Ϊx��y=0��
��ѡA��
���� ���⿼��˫���ߵķ��������ʣ��������Ǻ�����ͼ�������ʣ����ڻ����⣮


 ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
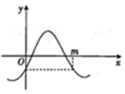
| A�� | 1 | B�� | $\frac{4}{3}$ | C�� | 2 | D�� | $\frac{4}{3}$��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | i | B�� | -2i | C�� | 2i | D�� | -i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{5}}{2}$ | B�� | -$\frac{\sqrt{10}}{2}$ | C�� | -$\frac{\sqrt{5}}{2}$ | D�� | $\frac{\sqrt{10}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��ֱ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | $4\sqrt{3}$ | C�� | 8 | D�� | $8\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
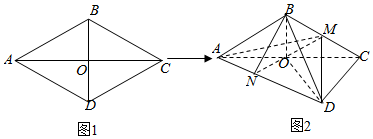
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com