
分析 求出m的范围判断①;举例说明②错误;由减函数可知f(x)在两段上均为减函数,且在第一段的最小值大于或等于第二段上的最大值,作出|f(x)|和y=2-$\frac{x}{3}$的图象,根据交点个数判断3a与2的大小关系,列出不等式组解出x的范围判断③;由a>0,b>-1,且a+b=1,变形可得$\frac{{a}^{2}+2}{a}$+$\frac{{b}^{2}}{b+1}$=$\frac{2}{a}+a$+b-1+$\frac{1}{b+1}$=$\frac{2}{a}+\frac{1}{2-a}$=f(a),0<a<2.利用导数求其最值判断④;由三角形的外心和重心的概念,可得O既是外心也为重心,则有△BCD为圆O:x2+y2=1的内接等边三角形,又$\overrightarrow{AD}•\overrightarrow{OB}$=($\overrightarrow{OD}-\overrightarrow{OA}$)•$\overrightarrow{OB}$,由向量的数量积的定义和余弦函数的值域,即可得到所求范围判断⑤.
解答 解:①当m=0时,关于x的不等式mx2+mx+2>0的解集为R,当m≠0时,
要使不等式mx2+mx+2>0的解集为R,则$\left\{\begin{array}{l}{m>0}\\{{m}^{2}-8m<0}\end{array}\right.$,解得0<m<8,综上,m的范围为0≤m<8,∴①错误;
②等比数列{an}的前n项和为Sn,则Sn、S2n-Sn、S3n-S2n也构成等比数列错误,如1,-1,1,-1,1,-1的前两项和、中两项和及后两项和,组成的数列为0,0,0.显然不是等比数列;
③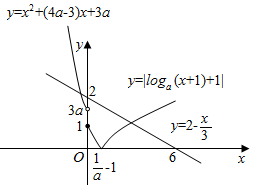 ∵f(x)是R上的单调递减函数,
∵f(x)是R上的单调递减函数,
∴y=x2+(4a-3)x+3a在(-∞,0)上单调递减,
y=loga(x+1)+1在(0,+∞)上单调递减,
且f(x)在(-∞,0)上的最小值大于或等于f(0).
∴$\left\{\begin{array}{l}{\frac{3-4a}{2}≥0}\\{0<a<1}\\{3a≥1}\end{array}\right.$,解得$\frac{1}{3}$≤a≤$\frac{3}{4}$.
作出y=|f(x)|和y=2-$\frac{x}{3}$的函数草图如图所示:
∵|f(x)|=2-$\frac{x}{3}$恰有两个不相等的实数解,
∴3a<2,即a<$\frac{2}{3}$.
综上,$\frac{1}{3}$≤a<$\frac{2}{3}$,故③错误;
④∵a>0,b>-1,且a+b=1,∴$\frac{{a}^{2}+2}{a}$+$\frac{{b}^{2}}{b+1}$=$a+\frac{2}{a}+b-1+\frac{1}{b+1}$=$\frac{2}{a}+\frac{1}{2-a}$=f(a),0<a<2.
令f′(a)=$-\frac{2}{{a}^{2}}+\frac{1}{(2-a)^{2}}=\frac{-({a}^{2}-8a+8)}{{a}^{2}(2-a)^{2}}$>0,解得4-2$\sqrt{2}$<a<2,此时函数f(a)单调递增;令f′(a)<0,解得0<a<4-2$\sqrt{2}$,此时函数f(a)单调递减.
∴当且仅当a=4-2$\sqrt{2}$时,函数f(a)取得极小值即最小值,f(4-2$\sqrt{2}$)=$\frac{3+2\sqrt{2}}{2}$,故④正确;
⑤由|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|=|$\overrightarrow{OD}$|=1,可知O为外心,由$\overrightarrow{OB}$+$\overrightarrow{OC}$+$\overrightarrow{OD}$=$\overrightarrow{0}$,可知O又为重心.
则有△BCD为圆O:x2+y2=1的内接等边三角形,
即有$\overrightarrow{AD}•\overrightarrow{OB}$=($\overrightarrow{OD}-\overrightarrow{OA}$)•$\overrightarrow{OB}$=$\overrightarrow{OB}•\overrightarrow{OD}$-$\overrightarrow{OA}•\overrightarrow{OB}$=|$\overrightarrow{OD}$|•|$\overrightarrow{OB}$|cos120°-|$\overrightarrow{OA}$|•|$\overrightarrow{OB}$|cos<$\overrightarrow{OA},\overrightarrow{OB}$>
=-$\frac{1}{2}$-$\sqrt{2}$cos<$\overrightarrow{OA},\overrightarrow{OB}$>,由于0≤<$\overrightarrow{OA},\overrightarrow{OB}$>≤π,
则-1≤cos<$\overrightarrow{OA},\overrightarrow{OB}$>≤1,
即有$\overrightarrow{AD}•\overrightarrow{OB}$∈$[{-\frac{1}{2}-\sqrt{2},-\frac{1}{2}+\sqrt{2}}]$,故⑤正确.
∴正确命题是④⑤.
故答案为:④⑤.
点评 本题考查命题的真假判断与应用,考查恒成立问题的求解方法,训练了利用导数求函数的最值,考查平面向量的应用,综合性强,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,-3) | B. | $(-\sqrt{3},3)$ | C. | $(\sqrt{3},-3)$ | D. | $(3,-\sqrt{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (0,1] | C. | (-∞,$\frac{5}{2}$) | D. | (-∞,$\frac{5}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{5}}{3}$ | D. | $\frac{\sqrt{7}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 过圆心 | B. | 相交而不过圆心 | C. | 相切 | D. | 相离 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
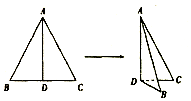 如图,将边长为2的正△ABC沿着高AD折起,使∠BDC=60°,若折起后A、B、C、D四点都在球O的表面上,则球O的表面积为( )
如图,将边长为2的正△ABC沿着高AD折起,使∠BDC=60°,若折起后A、B、C、D四点都在球O的表面上,则球O的表面积为( )| A. | $\frac{13}{2}π$ | B. | $\frac{13}{3}π$ | C. | $\frac{{13\sqrt{3}}}{2}π$ | D. | $\frac{{13\sqrt{3}}}{3}π$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com