
分析 由集合A={z||z一2|≤2,z∈C},可得:集合A表示以(2,0)为圆心,2为半径的圆及圆内部.B:由w=$\frac{1}{2}$zi+b,可得z=-2i(w-b),利用|z-2|=|-2i|•|w-b-i|=2•|w-(b+i)|≤2,可得|w-(b+i)|≤1,根据两圆的位置关系即可得出.
解答 解:由集合A={z||z一2|≤2,z∈C},可得:集合A表示以(2,0)为圆心,2为半径的圆及圆内部.
B:∵w=$\frac{1}{2}$zi+b,∴z=-2i(w-b),
∴z-2=-2i(w-b)+2i•i=-2i(w-b-i),
∴|z-2|=|-2i|•|w-b-i|=2•|w-(b+i)|≤2,
∴|w-(b+i)|≤1,
∴B表示的点是以(b,1)为圆心,1为半径的圆及圆内部,
A∩B≠∅,有两个临界位置(两圆外切),临界位置左右两侧都是A∩B=∅,
两圆内切时,A∩B=B,圆心的距离=半径的差,即(b-2)2+12=(2-1)2,∴b=2,
点评 本题考查了复数的运算性质、圆的复数方程、两圆的位置关系,考查了数形结合方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
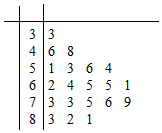 某公司做了用户对其产品満意度的问卷调查,随机抽取了20名用户的评分,得到图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意
某公司做了用户对其产品満意度的问卷调查,随机抽取了20名用户的评分,得到图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意| 不满意 | 满意 | 合计 | |
| 男 | 4 | 7 | |
| 女 | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{3}$,0) | B. | (-$\frac{1}{3}$,1) | C. | (0,2) | D. | (-$\frac{1}{3}$,log32) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com