
分析 可作出图形:分别取OB,OC的中点D,E,根据向量加法的平行四边形法则便知,点G的轨迹为以OD,OE为邻边的平行四边形,根据条件,由余弦定理可以求出BC=7,而根据正弦定理可以求出外接圆半径,从而可以得出OD,OE的值,这样根据三角形的面积公式即可求出点G的轨迹对应图形的面积为:2S△DOE.
解答 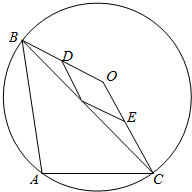 解:如图,取OB的中点D,OC的中点E,根据向量加法的平行四边形法则知,点G的轨迹为以OD,OE为邻边的平行四边形;
解:如图,取OB的中点D,OC的中点E,根据向量加法的平行四边形法则知,点G的轨迹为以OD,OE为邻边的平行四边形;
在△ABC中,∠A=120°,AB=5,AC=3;
∴由余弦定理得,BC2=52+32-2•5•3•cos120°=49;
∴BC=7;
由正弦定理,$\frac{BC}{sinA}=2r$;
即$\frac{7}{\frac{\sqrt{3}}{2}}=2r$;
∴$r=\frac{7}{\sqrt{3}}$;
∴$OD=OE=\frac{7}{2\sqrt{3}}$,且∠DOE=120°;
∴点G的轨迹对应图形面积为2S△DOE=OD•OE•sin∠DOE=$\frac{7}{2\sqrt{3}}•\frac{7}{2\sqrt{3}}•\frac{\sqrt{3}}{2}=\frac{49\sqrt{3}}{24}$.
故答案为:$\frac{49\sqrt{3}}{24}$.
点评 考查向量加法的平行四边形法则,余弦定理和正弦定理,以及三角形的面积公式:S=$\frac{1}{2}absinC$.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{4}$,$\frac{2π}{3}$] | B. | [-$\frac{π}{8}$,$\frac{π}{4}$] | C. | [-$\frac{π}{8}$,$\frac{2π}{3}$] | D. | [0,$\frac{2π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{25}{13}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若命题“p∧q”为假,则“p∨q”也为假 | |
| B. | 命题“?x0∈R,x${\;}_{0}^{2}$+x0+1<0”的否定是“?x∈R,x2+x+1<0” | |
| C. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
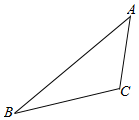 在△ABC中,AC=$\sqrt{2}$,AB=$\sqrt{3}$+1,∠BAC=45°,点P满足:$\overrightarrow{BP}$=(1-λ)$\overrightarrow{BA}$+λ$\overrightarrow{BC}$(λ>0),AP=$\frac{\sqrt{2}}{2}$.
在△ABC中,AC=$\sqrt{2}$,AB=$\sqrt{3}$+1,∠BAC=45°,点P满足:$\overrightarrow{BP}$=(1-λ)$\overrightarrow{BA}$+λ$\overrightarrow{BC}$(λ>0),AP=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A1C和AB1,BC1都垂直 | B. | A1C和AB1垂直,和BC1不垂直 | ||
| C. | A1C和AB1,BC1都不垂直 | D. | A1C和AB1不垂直,和BC1垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com