
分析 (1)先求函数h(x)的定义域,求出函数h(x)的导数,从而讨论判断函数的单调性;(2)分类讨论函数的单调性,从而化存在性问题为最值问题,从而解得.
解答 解:(1)函数h(x)=x-alnx+$\frac{1+a}{x}$的定义域为(0,+∞),
h′(x)=1-$\frac{a}{x}$-$\frac{1+a}{{x}^{2}}$=$\frac{(x+1)[x-(1+a)]}{{x}^{2}}$,
①当1+a≤0,即a≤-1时,
h′(x)>0,
故h(x)在(0,+∞)上是增函数;
②当1+a>0,即a>-1时,
x∈(0,1+a)时,h′(x)<0;x∈(1+a,+∞)时,h′(x)>0;
故h(x)在(0,1+a)上是减函数,在(1+a,+∞)上是增函数;
(2)由(1)令h(x0)=f(x0)-g(x0),x0∈[1,e],
①当a≤-1时,
存在x0∈[1,e](e=2.718…),使得h(x0)<0成立可化为
h(1)=1+1+a<0,
解得,a<-2;
②当-1<a≤0时,
存在x0∈[1,e](e=2.718…),使得h(x0)<0成立可化为
h(1)=1+1+a<0,解得,a<-2;
③当0<a≤e-1时,
存在x0∈[1,e](e=2.718…),使得h(x0)<0成立可化为
h(1+a)=1+a-aln(1+a)+1<0,无解;
④当e-1<a时,
存在x0∈[1,e](e=2.718…),使得h(x0)<0成立可化为
h(e)=e-a+$\frac{1+a}{e}$<0,
解得,a>$\frac{{e}^{2}+1}{e-1}$;
综上所述,
a的取值范围为(-∞,-2)∪($\frac{{e}^{2}+1}{e-1}$,+∞).
点评 本题考查了导数的综合应用及存在性问题的应用,同时考查了分类讨论的思想应用,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
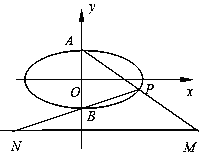 如图,已知椭圆$C:\frac{x^2}{4}+{y^2}=1$的上、下顶点分别为A,B,点P在椭圆上,且异于点A,B,直线AP,BP与直线l:y=-2分别交于点M,N,
如图,已知椭圆$C:\frac{x^2}{4}+{y^2}=1$的上、下顶点分别为A,B,点P在椭圆上,且异于点A,B,直线AP,BP与直线l:y=-2分别交于点M,N,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
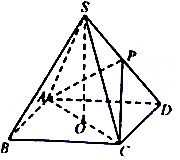 如图,在四棱锥S-ABCD中,点O是正方形ABCD的中心,SO⊥平面ABCD,且SO=OD,点P为棱SD上一点.
如图,在四棱锥S-ABCD中,点O是正方形ABCD的中心,SO⊥平面ABCD,且SO=OD,点P为棱SD上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{24}$+$\frac{1}{2}$kπ,$\frac{π}{8}$+$\frac{1}{2}$kπ),k∈Z | B. | (-$\frac{π}{8}$+$\frac{1}{2}$kπ,$\frac{π}{24}$+$\frac{1}{2}$kπ),k∈Z | ||
| C. | [$\frac{π}{24}$+kπ,$\frac{π}{8}$+kπ),k∈Z | D. | [$\frac{π}{24}$+kπ,$\frac{π}{8}$+kπ],k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (-∞,-1]∪[2,+∞) | C. | [-1,2] | D. | (-∞,-1)∪(2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com