
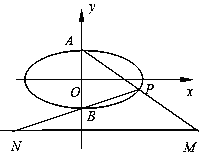
 如图,已知椭圆$C:\frac{x^2}{4}+{y^2}=1$的上、下顶点分别为A,B,点P在椭圆上,且异于点A,B,直线AP,BP与直线l:y=-2分别交于点M,N,
如图,已知椭圆$C:\frac{x^2}{4}+{y^2}=1$的上、下顶点分别为A,B,点P在椭圆上,且异于点A,B,直线AP,BP与直线l:y=-2分别交于点M,N,分析 (Ⅰ)由椭圆方程求出两个顶点A,B的坐标,设出P点坐标,写出直线AP、BP的斜率k1,k2,结合P的坐标适合椭圆方程可证结论;
(Ⅱ)分别求出M和N点的坐标,由(Ⅰ)中的结论得到两直线斜率间的关系,把|MN|用含有一个字母的代数式表示,然后利用基本不等式求最值.
解答 (Ⅰ)证明:由题设椭圆C:$\frac{{x}^{2}}{4}+{y}^{2}=1$可知,点A(0,1),B(0,-1).
令P(x0,y0),则由题设可知x0≠0.
∴直线AP的斜率${k}_{1}=\frac{{y}_{0}-1}{{x}_{0}}$,PB的斜率为${k}_{2}=\frac{{y}_{0}+1}{{x}_{0}}$.
又点P在椭圆上,
$\frac{{{x}_{0}}^{2}}{4}+{{y}_{0}}^{2}=1$(x0≠0),从而有${k}_{1}•{k}_{2}=\frac{{y}_{0}-1}{{x}_{0}}•\frac{{y}_{0}+1}{{x}_{0}}$=$\frac{{{y}_{0}}^{2}-1}{{{x}_{0}}^{2}}$=$-\frac{1}{4}$;
(Ⅱ)解:由题设可得直线AP的方程为y-1=k1(x-0),
直线PB的方程为y-(-1)=k2(x-0).
由$\left\{\begin{array}{l}{y-1={k}_{1}x}\\{y=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-\frac{3}{{k}_{1}}}\\{y=-2}\end{array}\right.$;
由$\left\{\begin{array}{l}{y+1={k}_{2}x}\\{y=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-\frac{1}{{k}_{2}}}\\{y=-2}\end{array}\right.$.
∴直线AP与直线l的交点N(-$\frac{3}{{k}_{1}}$,-2),直线PB与直线l的交点M(-$\frac{1}{{k}_{2}}$,-2).
∴|MN|=|$\frac{3}{{k}_{1}}-\frac{1}{{k}_{2}}$|,又${k}_{1}•{k}_{2}=-\frac{1}{4}$.
∴|MN|=|$\frac{3}{{k}_{1}}$+4k1|=$\frac{3}{|{k}_{1}|}$+4|k1|≥2$\sqrt{\frac{3}{|{k}_{1}|}•4|{k}_{1}|}$=4$\sqrt{3}$.
等号成立的条件是$\frac{3}{|{k}_{1}|}=4|{k}_{1}|$,即k1=±$\frac{\sqrt{3}}{2}$.
故线段MN长的最小值为4$\sqrt{3}$.
点评 本题考查了直线的斜率,考查了直线与圆锥曲线的关系,训练了代入法,考查了利用基本不等式求最值,考查了圆系方程,考查了学生的计算能力,是有一定难度题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
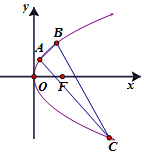 给定直线l:y=2x-16,抛物线G:y2=ax(a>0)
给定直线l:y=2x-16,抛物线G:y2=ax(a>0)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
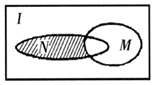 设全集I是实数集R,M={x|x≥3}与N={x|(x-3)(x-1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )
设全集I是实数集R,M={x|x≥3}与N={x|(x-3)(x-1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )| A. | {x|1<x<3} | B. | {x|1≤x<3} | C. | {x|1<x≤3} | D. | {x|1≤x≤3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com