
分析 (1)运用向量共线的坐标表示,可得x的方程,解方程即可;
(2)运用向量的坐标运算和数量积的坐标表示,结合二次函数的最值求法,即可得到所求范围.
解答 解:(1)因为向量$\vec a=({1,2-x})$,$\vec b=({1+x,2})$,$\vec a∥\vec b$,
所以(2-x)(1+x)=1×2,即为x2-x=0
解得x=0或x=1;
(2)因为$\vec a=({1,2-x})$,$\vec b=({1+x,2})$,所以$\vec a-\vec b=({-x,-x})$,
所以$\vec a•({\vec a-\vec b})=-x+({-x})({2-x})={x^2}-3x={({x-\frac{3}{2}})^2}-\frac{9}{4}$,
因为x∈[0,2],当x=$\frac{3}{2}$时取得最小值-$\frac{9}{4}$,当x=0时,x2-3x=0;当x=2时,x2-3x=-2,
可得最大值为0,
所以$\vec a•({\vec a-\vec b})$的取值范围$[{-\frac{9}{4},0}]$.
点评 本题考查向量共线的坐标表示和向量数量积的坐标表示,同时考查二次函数在闭区间上的最值求法,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x≤0,x2-x>0 | B. | ?x>0,x2-x≤0 | C. | ?x≤0,x2-x>0 | D. | ?x>0,x2-x<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
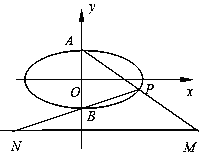 如图,已知椭圆$C:\frac{x^2}{4}+{y^2}=1$的上、下顶点分别为A,B,点P在椭圆上,且异于点A,B,直线AP,BP与直线l:y=-2分别交于点M,N,
如图,已知椭圆$C:\frac{x^2}{4}+{y^2}=1$的上、下顶点分别为A,B,点P在椭圆上,且异于点A,B,直线AP,BP与直线l:y=-2分别交于点M,N,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com