
分析 直接利用两条平行直线间的距离公式,点到直线的距离公式运算求得结果.
解答 解:∵l1:2x+y-1=0,l2:2x+y+1=0,
∴l1,l2的距离d=$\frac{|1-(-1)|}{\sqrt{4+1}}$=$\frac{2\sqrt{5}}{5}$;
点(0,2)到直线l1的距离d=$\frac{|2-1|}{\sqrt{5}}$=$\frac{{\sqrt{5}}}{5}$;
故答案为:$\frac{2\sqrt{5}}{5}$,$\frac{\sqrt{5}}{5}$.
点评 本题主要考查两条平行直线间的距离公式以及点到直线的距离公式的应用,注意未知数的系数相同,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,一个正六角星薄片(其对称轴与水面垂直)匀速地升出水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(t)的图象大致为( )
如图,一个正六角星薄片(其对称轴与水面垂直)匀速地升出水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(t)的图象大致为( )| A. | 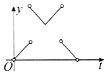 | B. |  | C. | 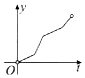 | D. | 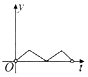 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com