
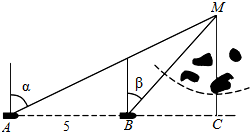
 如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行.
如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行.分析 (Ⅰ)在△ABM中可知,AB=BM=5,求出MC与3比较,即可得到结论;
(Ⅱ)在△ABM中由正弦定理得可得MC,当且仅当MC>3时没有触礁危险.
解答 解:(Ⅰ)在△ABM中可知,AB=BM=5,…4分
从而MC=5sin60°=$\frac{5}{2}\sqrt{3}$>3,没有触礁危险.…8分
(Ⅱ)设CM=x,在△ABM中由正弦定理得,$\frac{5}{sin(α-β)}=\frac{x}{cosαcosβ}$,
解得x=$\frac{5cosαcosβ}{sin(α-β)}$,…14分
所以当$\frac{5cosαcosβ}{sin(α-β)}$>3时没有触礁危险.…16分.
点评 本题考查利用数学知识解决实际问题,考查学生分析解决问题轭能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (n-1)•2n+1 | B. | $\frac{n+2}{{2}^{n-1}}$-2 | C. | $\frac{2-n}{{2}^{n-1}}$ | D. | 4-$\frac{n+2}{{2}^{n-1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | $-\frac{9}{4}$ | D. | $\frac{9}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $arcsin\frac{{\sqrt{3}}}{5}$ | B. | arcsin(-$\frac{\sqrt{3}}{5}$) | C. | π-arcsin$\frac{{\sqrt{3}}}{5}$ | D. | $\frac{π}{2}+arcsin\frac{{\sqrt{3}}}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com