
分析 (1)直接利用诱导公式化简求解即可得到f(α);
(2)利用$f(θ-\frac{π}{3})=-\frac{1}{7}$,$-\frac{π}{2}<θ<\frac{π}{2}$,结合三角函数的基本关系式,求出余弦函数值,然后求cos2θ的值.
解答 解:(1)$f(α)=\frac{{sin(α-π)cos(2π-α)cos(-α+\frac{3}{2}π)}}{{cos(\frac{π}{2}-α)sin(-π-α)}}$=$\frac{sinαcosαsinα}{sinαsinα}$=cosα.
∴f(α)=cosα…(6分)
(2)∵f(α)=cosα,$f(θ-\frac{π}{3})=-\frac{1}{7}$,可得cos($θ-\frac{π}{3}$)=$-\frac{1}{7}$,
$\frac{1}{2}cosθ+\frac{\sqrt{3}}{2}sinθ=-\frac{1}{7}$,sin2θ+cos2θ=1,$-\frac{π}{2}<θ<\frac{π}{2}$,解得$cosθ=\frac{11}{14}$,
∴$cos2θ=2{cos}^{2}θ-1=\frac{23}{98}$…(6分)
点评 本题考查诱导公式的应用,两角和与差的三角函数,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | 2+$\sqrt{6}$ | D. | 2-$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
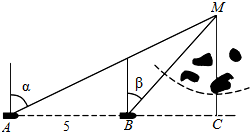 如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行.
如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 焦点在x轴上的椭圆 | B. | 焦点在y轴上的椭圆 | ||
| C. | 焦点在x轴上的双曲线 | D. | 焦点在y轴上的双曲线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 由曲线y=sinx,y=cosx与直线x=0,x=$\frac{π}{2}$所围成的平面图形(下图中的阴影部分)的面积是2$\sqrt{2}$-2.
由曲线y=sinx,y=cosx与直线x=0,x=$\frac{π}{2}$所围成的平面图形(下图中的阴影部分)的面积是2$\sqrt{2}$-2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com