
| A. | (n-1)•2n+1 | B. | $\frac{n+2}{{2}^{n-1}}$-2 | C. | $\frac{2-n}{{2}^{n-1}}$ | D. | 4-$\frac{n+2}{{2}^{n-1}}$ |
分析 利用导数的几何意义,可得数列{an}是以1为首项,$\frac{1}{2}$为公比的等比数列,an=$\frac{1}{{2}^{n-1}}$;根据数列{bn}满足|QnF|=nbn+$\frac{1}{4}$,可得n2+$\frac{1}{4}$=nbn+$\frac{1}{4}$,bn=n,再利用错位相减法,即可求出数列{anbn}的前n项和
解答 解:∵y=x2,∴y′=2x,
则2an=an-1,
∵a1=1,∴数列{an}是以1为首项,$\frac{1}{2}$为公比的等比数列,
∴an=$\frac{1}{{2}^{n-1}}$;
∵数列{bn}满足|QnF|=nbn+$\frac{1}{4}$,
∴n2+$\frac{1}{4}$=nbn+$\frac{1}{4}$,
∴bn=n,
∴anbn=$\frac{n}{{2}^{n-1}}$
∵Sn=1+2•$\frac{1}{2}$+…+$\frac{n}{{2}^{n-1}}$,
∴$\frac{1}{2}$Sn=$\frac{1}{2}$+2•$\frac{1}{{2}^{2}}$+…+$\frac{n}{{2}^{n}}$,
两式相减,整理可得Sn=4-$\frac{n+2}{{2}^{n-1}}$.
故选:D.
点评 本题考查导数的几何意义,考查抛物线的定义,考查数列的求和,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
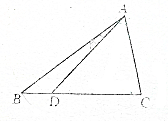 如图,在直角三角形ABC中,∠C=90°,D为BC边上的一点,且BC=4BD,设∠CAD=α,∠BAD=β,若tanα=7tanβ,求角α的大小.
如图,在直角三角形ABC中,∠C=90°,D为BC边上的一点,且BC=4BD,设∠CAD=α,∠BAD=β,若tanα=7tanβ,求角α的大小.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
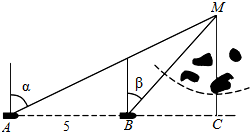 如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行.
如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com