
分析 设出指数函数解析式,将点的坐标代入,求参数a,然后将不等式具体化,换元得到一元二次不等式解之,然后还原求解集.
解答 解:设指数函数解析式为y=ax,因为指数函数f(x)的图象过点(-2,4),所以4=a-2,解得a=$\frac{1}{2}$,所以指数函数解析式为y=$(\frac{1}{2})^{x}$,所以f(3)=$(\frac{1}{2})^{3}=\frac{1}{8}$;
不等式f(x)+f(-x)<$\frac{5}{2}$为$(\frac{1}{2})^{x}+{2}^{x}<\frac{5}{2}$,设2x=t,不等式化为$\frac{1}{t}+t<\frac{5}{2}$,所以2t2-5t+2<0解得$\frac{1}{2}$<t<2,即$\frac{1}{2}$<2x<2,所以-1<x<1,所以不等式的解集为(-1,1).
故答案为:$\frac{1}{8}$;(-1,1).
点评 本题考查了待定系数法求指数函数解析式以及解指数不等式;采用了换元的方法.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 类别 | A | B | C |
| 数量 | 4 | 3 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知PA⊥平面ABCD,CD⊥AD,BA⊥AD,CD=AD=AP=4,AB=2.
已知PA⊥平面ABCD,CD⊥AD,BA⊥AD,CD=AD=AP=4,AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
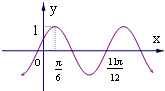 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象,如图所示,则将y=f(x)的图象向右平移$\frac{π}{3}$个单位后,得到的图象解析式为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象,如图所示,则将y=f(x)的图象向右平移$\frac{π}{3}$个单位后,得到的图象解析式为( )| A. | y=sin(2x-$\frac{π}{6}$) | B. | y=cos2x | C. | y=sin(2x+$\frac{5π}{6}$) | D. | y=-cos2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知f(x)=Asin(ωx+φ)(x∈R)的图象的一部分如图所示,若对任意x∈R都有f(x1)≤f(x)≤f(x2),则|x1-x2|的最小值为( )
已知f(x)=Asin(ωx+φ)(x∈R)的图象的一部分如图所示,若对任意x∈R都有f(x1)≤f(x)≤f(x2),则|x1-x2|的最小值为( )| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com