
分析 (1)求出函数的导数,结合x的范围,求出函数的单调区间,从而求出函数的最小值即可;
(2)问题转化为只需证明:x-y+1≥$\frac{x}{y}$,即证明:xy-y2+y-x≥0,而xy-y2+y-x=y(x-y)-(x-y)=(x-y)(y-1),从而证出结论;
(3)假设存在,得到方程(x-1)2ex=x有两个大于1的不等实根,设函数G(x)=(x-1)2ex-x(x>1),根据函数的单调性得到G(x)在(1,+∞)上仅有一个零点,得到矛盾,从而判断结论.
解答 解:(1)h(x)=ex-1-lnx-1(x≥1),h′(x)=ex-1-$\frac{1}{x}$,
∵x∈[1,+∞),∴ex-1≥1,$\frac{1}{x}$∈(0,1],
∴h′(x)≥0,
∴函数h(x)在区间[1,+∞)上单调递增,
∴h(x)min=h(1)=0;
(2)由(1)知,当x≥1时,ex-1-1≥lnx且当x=1时取等号,
∵1≤y<x,∴x-y+1>1
∴ex-y+1-1-1>ln(x-y+1),要证明ex-y-1>lnx-lny,
只需证明:ln(x-y+1)≥lnx-lny,只需证明:x-y+1≥$\frac{x}{y}$,
即证明:xy-y2+y-x≥0,而xy-y2+y-x=y(x-y)-(x-y)=(x-y)(y-1),
∵1≤y<x,∴x-y>0,y-1≥0,∴xy-y2+y-x=(x-y)(y-1)≥0,得证.
∴当1≤y<x时,ex-y-1>lnx-lny.
(3)H(x)=(x-1)2f(x),H′(x)=(x2-1)ex
假设存在区间[a,b](a>1),使函数H(x)在区间[a,b]的值域也是[a,b],
当x>1时,H′(x)>0,所以函数在区间(1,+∞)单调递增,
故 $\left\{\begin{array}{l}{H(a){{=(e-1)}^{2}e}^{a}=a}\\{H(b){{=(b-1)}^{2}e}^{b}=b}\end{array}\right.$,即方程(x-1)2ex=x有两个大于1的不等实根,
设函数G(x)=(x-1)2ex-x(x>1),则G′(x)=(x2-1)ex-1,G′′(x)=(x2+2x-1)ex,
当x>1时,G′′(x)>0,即函数G′(x)=(x2-1)ex-1在区间(1,+∞)单调递增,
又G′(1)=-1<0,G′(2)=3e2-1>0,所以存在唯一的x0∈(1,2)使得G′(x0)=0,
当x∈(1,x0)时,G′(x)<0,函数G(x)递减,当x∈(x0,+∞)时,G′(x)>0,函数G(x)递增,
所以函数G(x)有极小值G(x0)<G(1)=-1,G(2)=e2-2>0,
所以函数G(x)在(1,+∞)上仅有一个零点,
这与方程(x-1)2ex=x有两个大于1的不等实根矛盾,
故不存在区间[a,b](a>1),使函数H(x)在区间[a,b]的值域也是[a,b].
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,是一道综合题.


科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 45° | C. | 75° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M?N | B. | N?M | C. | M∩N=ϕ | D. | M=N |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
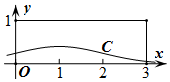 在如图所示的矩形中随机投掷30000个点,则落在曲线C下方(曲线C为正态分布N(1,1)的正态曲线)的点的个数的估计值为( )
在如图所示的矩形中随机投掷30000个点,则落在曲线C下方(曲线C为正态分布N(1,1)的正态曲线)的点的个数的估计值为( )| A. | 4985 | B. | 8185 | C. | 9970 | D. | 24555 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{8}$ | C. | $1-\frac{π}{4}$ | D. | $1-\frac{π}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 印刷册数 (千册) | 2 | 3 | 4 | 5 | 8 |
| 单册成本 (元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
| 印刷册数x(千册) | 2 | 3 | 4 | 5 | 8 | |
| 单册成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
| 模型甲 | 估计值${\stackrel{∧}{{y}_{i}}}^{(1)}$ | 2.4 | 2.1 | 1.6 | ||
| 残差${\stackrel{∧}{{e}_{i}}}^{(1)}$ | 0 | -0.1 | 0.1 | |||
| 模型乙 | 估计值 ${\stackrel{∧}{{y}_{i}}}^{(2)}$ | 2.3 | 2 | 1.9 | ||
| 残差 ${\stackrel{∧}{{e}_{i}}}^{(2)}$ | 0.1 | 0 | 0 | |||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com