
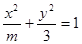 的右焦点与抛物线
的右焦点与抛物线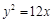 的焦点重合,则
的焦点重合,则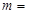
| A.3 | B.6 | C.9 | D.12 |
科目:高中数学 来源:不详 题型:解答题
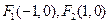 的椭圆经过点
的椭圆经过点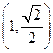 , 直线
, 直线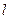 过点
过点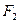 与椭圆交于
与椭圆交于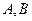 两点, 其中
两点, 其中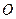 为坐标原点.
为坐标原点.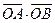 的范围;
的范围; 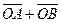 与向量
与向量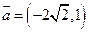 共线, 求
共线, 求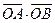 的值及
的值及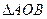 的外接圆方程.
的外接圆方程. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
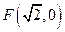 ,且经过点
,且经过点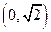
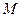 、
、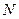 是直线
是直线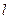 :
: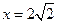 上的两个动点,点
上的两个动点,点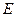 与点
与点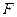 关于原点
关于原点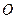 对称,若
对称,若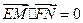 ,求
,求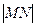 的最小值。
的最小值。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
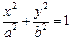 的焦点F,且与椭圆交于相异的两点A、B,则
的焦点F,且与椭圆交于相异的两点A、B,则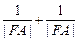 等于常数
等于常数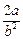 ” 可以类比推出抛物线的类似性质是“若直线l过抛物线
” 可以类比推出抛物线的类似性质是“若直线l过抛物线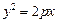 的焦点F,且与抛物线交于相异的两点A、B,则
的焦点F,且与抛物线交于相异的两点A、B,则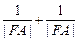 等于常数” .
等于常数” .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com