
| 分组 | 频数 | 频率 |
| [485.5,490.5) | 10 | y1 |
| [490.5,495.5) | x1 | y2 |
| [495.5,500.5) | x2 | y3 |
| 10 | ||
| 合计 | 100 |
分析 (1)根据题意,频率等于频数除以样本容量,那么可知随机抽取了100袋,以每5克为一个组来分为4组来得到频率值0.1,0.3,0.5,0.1,进而得到频率分布表,利用频率分布表作出频率分布直方图.(2)由频率分布直方图知中位数应在第三组设中位数为x,由0.1+0.3+0.1(x-495.5)=0.5,能求出这100包白糖重量的中位数为496.5g.
解答 解:(1)根据题意,频率等于频数除以样本容量,那么可知随机抽取了100袋,以每5克为一个组来分为4组来得到频率值0.1,0.3,0.5,0.1,进而得到表格.
| 分组 | 频数 | 频率 |
| [485.5,490.5) | 10 | 0.1 |
| [490.5,495.5) | 30 | 0.3 |
| [495.5,500.5) | 50 | 0.5 |
| 10 | 0.1 | |
| 合计 | 100 | 1 |
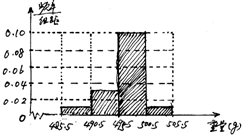
点评 本题考查频率分布直方图的作法,考查中位数的求法,是基础题,解题时要认真审题,注意频率分布直方图的性质的合理运用.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p是q的充分不必要条件 | |
| B. | p是q的充分条件,但不是q的必要条件 | |
| C. | p是q的必要条件,但不是q的充分条件 | |
| D. | p既不是q的必要条件,也不是q的充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
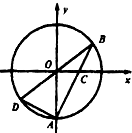 已知圆O:x2+y2=r2(r>0)及圆上的点A(0,-r),过点A的直线l交圆于另一点B,交x轴于点C,若OC=BC,则直线l的斜率为±$\sqrt{3}$.
已知圆O:x2+y2=r2(r>0)及圆上的点A(0,-r),过点A的直线l交圆于另一点B,交x轴于点C,若OC=BC,则直线l的斜率为±$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
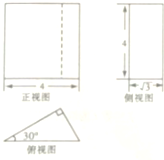
| A. | 24+8$\sqrt{3}$ | B. | 16=12$\sqrt{3}$ | C. | 24+12$\sqrt{3}$ | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=sin(x-\frac{π}{4})$ | B. | $y=cos(x+\frac{π}{4})$ | C. | $y=sin(2x+\frac{π}{4})$ | D. | $y=cos(2x-\frac{π}{4})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com