
分析 (1)本题是一个古典概型,试验发生包含的事件a,b都从0,1,2,3四个数中任取的一个数的基本事件总数为5×5个,函数有零点的条件为△=a2-4b≥0,即a2≥4b,列举出所有事件的结果数,得到概率.
(2)由题意知本题是一个几何概型,试验发生包含的事件可以写出a,b满足的条件,满足条件的事件也可以写出,画出图形,做出两个事件对应的图形的面积,得到比值
解答 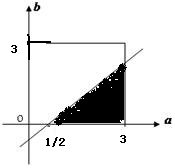 解:(1)由题意知本题是一个古典概型,
解:(1)由题意知本题是一个古典概型,
试验发生包含的事件a,b都从0,1,2,3四个数中任取的一个数的
基本事件总数为N=4×4=16个,
函数有零点的条件为△,4a2-8b≥0,即a2≥2
∵事件“a2≥2b”包含:(0,0),(2,0),
(2,1),(2,2)(3,0),(3,1),(3,2),(3,3)共有7个
∴事件“a2≥2b”的概率为p=$\frac{7}{16}$;
(2)f(1)=1-2a+2b<0,∴a-b>$\frac{1}{2}$
则a,b都是从区间[0,3]任取的一个数,有f(1)<0,
即满足条件:$\left\{\begin{array}{l}{0≤a≤3}\\{0≤b≤3}\\{a-b>\frac{1}{2}}\end{array}\right.$
转化为几何概率如图所示,阴影部分面积为$\frac{1}{2}×\frac{5}{2}×\frac{5}{2}=\frac{25}{8}$
∴事件“f(1)<0”的概率为p=$\frac{\frac{25}{8}}{3×3}=\frac{25}{72}$.
点评 古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 广告费x | 2 | 3 | 4 | 5 | 6 |
| 销售额y | 29 | 41 | 50 | 59 | 71 |
| A. | 90.8 | B. | 72.4 | C. | 98.2 | D. | 111.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当x>0且x≠1时,lgx$+\frac{1}{lgx}$≥2 | B. | 6$-x-\frac{4}{x}$的最大值是2 | ||
| C. | $\frac{{x}^{2}+5}{\sqrt{{x}^{2}+4}}$的最小值是2 | D. | 当x∈(0,π)时,sinx$+\frac{4}{sinx}$≥5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com