
分析 (1)根据通项公式即可求出n的值,
(2)设展开式系数最大项为第r+1项,则得到关于r烦人不等式组,解得r,问题得以解决
解答 解:(1)展开式的通项公式为 Tr+1=2-n+2r•Cnrx${\;}^{\frac{n-3r}{2}}$,
∵展开式中第6项为常数,
∴r=5,
即为$\frac{n-15}{2}$=0,
解得n=15,
(2)设展开式系数最大项为第r+1项,则有2-15+2r•C15r≥2-13+2r•C15r+1,
2-15+2r•C15r≤2-17+2r•C15r-1,
解得r=12
故第13项的系数最大为2-15+24•C1512x${\;}^{\frac{15-3×12}{2}}$=29C153x${\;}^{-\frac{21}{2}}$
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $lg\frac{3}{n+3}$ | B. | $lg\frac{2}{n}$ | C. | $lg\frac{{3({n+1})}}{n+3}$ | D. | $lg\frac{{2({n+2})}}{n}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 增加2个单位 | B. | 减少2个单位 | C. | 增加3个单位 | D. | 减少3个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
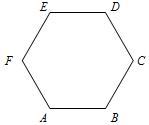 如图,点P是边长为1的正六边形ABCDEF的边上的一个动点,设$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AE}$,则x+y的最大值为2.
如图,点P是边长为1的正六边形ABCDEF的边上的一个动点,设$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AE}$,则x+y的最大值为2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com