Question

4£®ÒÑÖªÍÖÔ²C£º$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1£¨a£¾b£¾0£©µÄÀëÐÄÂÊ$\frac{\sqrt{5}}{3}$£¬F£¬AΪÍÖÔ²CµÄÓÒ½¹µãºÍÓÒ¶¥µã£¬B£¨0£¬b£©£¬ÇÒ$\frac{\sqrt{5}}{|OF|}$$+\frac{2}{|OA|}$=$\frac{12{e}^{2}}{|OB{|}^{2}}$
£¨1£©ÇóÍÖÔ²CµÄ·½³Ì£»
£¨2£©ÉèMÊǵÚÈýÏóÏÞÄÚÇÒÍÖÔ²ÉϵÄÒ»¸ö¶¯µã£¬Ö±ÏßMBÓëxÖá½»ÓÚµãP£¬Ö±ÏßMAÓëyÖá½»ÓÚµãQ£¬ÇóÖ¤£ºËıßÐÎABPQµÄÃæ»ýΪ¶¨Öµ£®

Answer 1

·ÖÎö £¨1£©ÓÉÍÖÔ²µÄÀëÐÄÂÊ$\frac{\sqrt{5}}{3}$£¬F£¬AΪÍÖÔ²CµÄÓÒ½¹µãºÍÓÒ¶¥µã£¬B£¨0£¬b£©£¬ÇÒ$\frac{\sqrt{5}}{|OF|}$$+\frac{2}{|OA|}$=$\frac{12{e}^{2}}{|OB{|}^{2}}$£¬Áгö·½³Ì×飬Çó³öa=3£¬b=2£¬c=$\sqrt{5}$£¬ÓÉ´ËÄÜÇó³öÍÖÔ²CµÄ·½³Ì£®
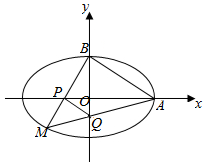
£¨2£©Çó³öA£¨3£¬0£©£¬B£¨0£¬2£©£¬ÉèM£¨m£¬n£©£¬£¨m£¼0£¬n£¼0£©£¬Ôò9n²+4m²=36£¬Ö±ÏßBMµÄ·½³ÌΪ$y=\frac{n-2}{m}x+2$£¬Áîy=0£¬µÃx_P=$\frac{2m}{2-n}$£¬Ö±ÏßAMµÄ·½³ÌΪ$y=\frac{n}{m-3}£¨x-3£©$£¬Áîx=0£¬µÃy_Q=$\frac{3n}{3-m}$£¬ËıßÐÎABPQµÄÃæ»ýΪ£ºS_{ËıßÐÎABPQ}=$\frac{1}{2}¡Á|AP|¡Á|BQ|$=$\frac{1}{2}¡Á£¨3-\frac{2m}{2-n}£©¡Á£¨2-\frac{3n}{3-m}£©$£¬ÓÉ´ËÄÜÖ¤Ã÷ËıßÐÎABPQµÄÃæ»ýΪ¶¨Öµ£®

½â´ð ½â£º£¨1£©¡ßÍÖÔ²C£º$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1£¨a£¾b£¾0£©µÄÀëÐÄÂÊ$\frac{\sqrt{5}}{3}$£¬
F£¬AΪÍÖÔ²CµÄÓÒ½¹µãºÍÓÒ¶¥µã£¬B£¨0£¬b£©£¬ÇÒ$\frac{\sqrt{5}}{|OF|}$$+\frac{2}{|OA|}$=$\frac{12{e}^{2}}{|OB{|}^{2}}$£¬
¡à$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{5}}{3}}\\{\frac{\sqrt{5}}{c}+\frac{2}{a}=\frac{12¡Á£¨\frac{\sqrt{5}}{3}£©^{2}}{{b}^{2}}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$£¬
½âµÃa=3£¬b=2£¬c=$\sqrt{5}$£¬
¡àÍÖÔ²CµÄ·½³ÌΪ$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}$=1£®
£¨2£©Ö¤Ã÷£º¡ßÍÖÔ²CµÄ·½³ÌΪ$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}$=1£¬¡àA£¨3£¬0£©£¬B£¨0£¬2£©£¬
ÉèM£¨m£¬n£©£¬£¨m£¼0£¬n£¼0£©£¬Ôò$\frac{{m}^{2}}{9}+\frac{{n}^{2}}{4}$=1£¬¡à9n²+4m²=36£¬
Ö±ÏßBMµÄ·½³ÌΪ$y=\frac{n-2}{m}x+2$£¬Áîy=0£¬µÃx_P=$\frac{2m}{2-n}$£¬
Ö±ÏßAMµÄ·½³ÌΪ$y=\frac{n}{m-3}£¨x-3£©$£¬Áîx=0£¬µÃy_Q=$\frac{3n}{3-m}$£¬
¡àËıßÐÎABPQµÄÃæ»ýΪ£º
S_{ËıßÐÎABPQ}=$\frac{1}{2}¡Á|AP|¡Á|BQ|$
=$\frac{1}{2}¡Á£¨3-\frac{2m}{2-n}£©¡Á£¨2-\frac{3n}{3-m}£©$
=$\frac{1}{2}¡Á\frac{6-3n-2m}{2-n}¡Á\frac{6-2m-3n}{3-m}$
=$\frac{36+9{n}^{2}+4{m}^{2}-36n-24m+12mn}{12-6n-4m+2mn}$
=$\frac{72-36n-24m+12mn}{12-6n-4m+2mn}$=6£®
¡àËıßÐÎABPQµÄÃæ»ýΪ¶¨Öµ6£®

µãÆÀ ±¾Ì⿼²éÍÖÔ²·½³ÌµÄÇ󷨣¬¿¼²éËıßÐεÄÃæ»ýΪ¶¨ÖµµÄÖ¤Ã÷£¬¿¼²éÍÖÔ²¡¢Ö±Ïß·½³ÌµÈ»ù´¡ÖªÊ¶£¬¿¼²éÍÆÀíÂÛÖ¤ÄÜÁ¦¡¢ÔËËãÇó½âÄÜÁ¦£¬¿¼²é»¯¹éÓëת»¯Ë¼Ïë¡¢º¯ÊýÓë·½³Ì˼Ï룬ÊÇÖеµÌ⣮