
分析 (1)根据二项展开式的通项公式,结合第四项的未知数的幂指数等于零,求得n的值.
(2)本题即求${(\sqrt{x}+\frac{2}{\root{3}{x}})}^{n}$的各项系数和,令x=1,可得它的结果.
(3)设${(\sqrt{x}-\frac{2}{{\root{3}{x}}})^n}$展开式的第r+1项系数绝对值为Ar+1,且Ar+1为最大值,求得r的值,检验即可.
解答 解:(1)∵${(\sqrt{x}-\frac{2}{{\root{3}{x}}})^n}$的展开式中第四项为常数项,∴${T_4}=C_n^3{(\sqrt{x})^{n-3}}•{(-\frac{2}{{\root{3}{x}}})^3}=C_n^3{(-2)^3}{x^{\frac{n-5}{2}}}$,∴$\frac{n-5}{2}$=0,∴n=5.
(2)由(1)知n=5,∴${(\sqrt{x}-\frac{2}{{\root{3}{x}}})^n}$展开式的各项系数绝对值之和即${(\sqrt{x}+\frac{2}{\root{3}{x}})}^{n}$的各项系数和,
令x=1,可得${(\sqrt{x}+\frac{2}{\root{3}{x}})}^{n}$的各项系数和为35.
(3)设${(\sqrt{x}-\frac{2}{{\root{3}{x}}})^n}$展开式的第r+1项系数绝对值为Ar+1,且Ar+1为最大值,
则$\left\{\begin{array}{l}{A_{r+1}}≥{A_r}\\{A_{r+1}}≥{A_{r+2}}\end{array}\right.⇒\left\{\begin{array}{l}12-2r≥r\\ r+1≥10-2r\end{array}\right.⇒3≤r≤4$,∵r∈N*,∴r=3或4,
又∵r=3时,${(\sqrt{x}-\frac{2}{{\root{3}{x}}})^n}$是展开式中第四项,其系数是负值,∴r=4,
故${(\sqrt{x}-\frac{2}{{\root{3}{x}}})^n}$的展开式中系数最大的项为:${T_5}=C_5^4{(\sqrt{x})^1}•{(-\frac{2}{{\root{3}{x}}})^4}=C_5^4{(-2)^4}{x^{-\frac{5}{6}}}$.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于中档题.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1+y}{x}$和$\frac{1+x}{y}$都大于2 | B. | $\frac{1+y}{x}$和$\frac{1+x}{y}$都小于2 | ||
| C. | $\frac{1+y}{x}$和$\frac{1+x}{y}$中至少有一个小于2 | D. | 以上说法都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
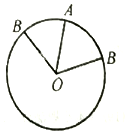 如图,点A为周长为3的圆周上的一定点,若在该圆周上随机取一点B,则劣弧AB的长度小于1的概率为( )
如图,点A为周长为3的圆周上的一定点,若在该圆周上随机取一点B,则劣弧AB的长度小于1的概率为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com