
分析 (Ⅰ)本题是古典概型,首先明确事件的个数,利用公式解答;
Ⅱ)本问是几何概型的求法,明确事件对应的区域面积,利用面积比求概率.
解答 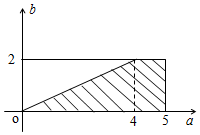 解:(Ⅰ)当a∈{0,1,2,3,4,5},b∈{0,1,2}时,共可以产生6×3=18个一元二次方程.
解:(Ⅰ)当a∈{0,1,2,3,4,5},b∈{0,1,2}时,共可以产生6×3=18个一元二次方程.
若事件A发生,则a 2-4b2≥0,即|a|≥2|b|.又a≥0,b≥0,所以a≥2b.(3分)
从而数对(a,b)的取值为(0,0),(1,0),(2,0),(2,1),(3,0),(3,1),(4,0),(4,1),(4,2),(5,0),(5,1),(5,2),共12组值.
所以P(A)=$\frac{12}{18}=\frac{2}{3}$.(5分)
(Ⅱ)据题意,试验的全部结果所构成的区域为D={(a,b)|0≤a≤5,0≤b≤2},构成事件A的区域为A={(a,b)|0≤a≤5,0≤b≤2,a≥2b}.(8分)
在平面直角坐标系中画出区域A、D,如图,
其中区域D为矩形,其面积S(D)=5×2=10,
区域A为直角梯形,其面积S(A)=$\frac{1+5}{2}×2=6$.(11分)
所以P(A)=$\frac{S(A)}{S(D)}=\frac{6}{10}=\frac{3}{5}$.(12分)
点评 古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点.
如图,四棱锥P-ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1)∪(2,3) | B. | [-1,1]∪[2,3] | C. | (1,2) | D. | R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校在“普及环保知识节”后,为了进一步增强环保意识,从本校学生中随机抽取了一批学生参加环保基础知识测试.经统计,这批学生测试的分数全部介于75至100之间.将数据分成以下5组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到如图所示的频率分布直方图.
某校在“普及环保知识节”后,为了进一步增强环保意识,从本校学生中随机抽取了一批学生参加环保基础知识测试.经统计,这批学生测试的分数全部介于75至100之间.将数据分成以下5组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到如图所示的频率分布直方图. 查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com