
分析 (1)分类讨论,即可解不等式f(x)≥2;
(2)因为|2x-1|+|x-a|≥|(2x-1)-(x-a)|=|x-1+a|.由绝对值不等式成立条件可知:当且仅当(2x-1)(x-a)≤0时成立,即可求x的取值范围.
解答 解:(1)当a=1时,f(x)=|2x-1|+|x-1|. …(1分)
当x≥1时,3x-2≥2,∴x≥$\frac{4}{3}$ …(2分)
当$\frac{1}{2}$≤x<1时,无解 …(3分)
当x<$\frac{1}{2}$时,x≤0 …(4分)
综上:不等式的解集为{x|x≤0或x≥$\frac{4}{3}$}; …(5分)
(2)因为|2x-1|+|x-a|≥|(2x-1)-(x-a)|=|x-1+a|. …(6分)
由绝对值不等式成立条件可知:
当且仅当(2x-1)(x-a)≤0时成立 …(7分)
当a>$\frac{1}{2}$时,$\frac{1}{2}≤x≤a$ …(8分)
当a=$\frac{1}{2}$时,x=$\frac{1}{2}$ …(9分)
当a<$\frac{1}{2}$时,a≤x≤$\frac{1}{2}$.…(10分)
点评 本题考查不等式的解法,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 40 | B. | 30 | C. | 20 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
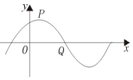 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,其中点P(1,2)为函数图象的一个最高点,Q(4,0)为函数图象与x轴的一个交点,O为坐标原点.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,其中点P(1,2)为函数图象的一个最高点,Q(4,0)为函数图象与x轴的一个交点,O为坐标原点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
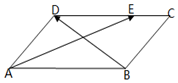 如图,在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,若$\overrightarrow{DE}=2\overrightarrow{EC}$,则$\overrightarrow{AE}•\overrightarrow{BD}$=-2.
如图,在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,若$\overrightarrow{DE}=2\overrightarrow{EC}$,则$\overrightarrow{AE}•\overrightarrow{BD}$=-2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com