
【题目】某家具厂有方木料90![]() ,五合板600
,五合板600![]() ,准备加工成书桌和书橱出售.已知生产第张书桌需要方木料O.l
,准备加工成书桌和书橱出售.已知生产第张书桌需要方木料O.l![]() ,五合板2
,五合板2![]() ,生产每个书橱而要方木料0.2
,生产每个书橱而要方木料0.2![]() ,五合板1
,五合板1![]() ,出售一张方桌可获利润80元,出售一个书橱可获利润120元.
,出售一张方桌可获利润80元,出售一个书橱可获利润120元.
(1)如果只安排生产书桌,可获利润多少?
(2)怎样安排生产可使所得利润最大?
【答案】(1) 只安排生产书桌,最多可生产300张书桌,获得利润24000元;(2) 生产书桌100张、书橱400个,可使所得利润最大
【解析】
(1)设只生产书桌x个,可获得利润z元,则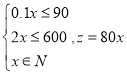 ,由此可得
,由此可得![]() 最大值;
最大值;
(2)设生产书桌x张,书橱y个,利润总额为z元.
则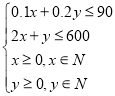 ,
,![]() ,由线性规划知识可求得
,由线性规划知识可求得![]() 的最大值.即作可行域,作直线
的最大值.即作可行域,作直线![]() ,平移此直线得最优解.
,平移此直线得最优解.
由题意可画表格如下:
方木料( | 五合板( | 利润(元) | |
书桌(个) | 0.1 | 2 | 80 |
书橱(个) | 0.2 | 1 | 120 |
(1)设只生产书桌x个,可获得利润z元,
则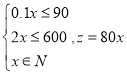 , ∴
, ∴![]() ∴
∴![]()
所以当![]() 时,
时,![]() (元),即如果只安排生产书桌,最多可生产300张书桌,获得利润24000元
(元),即如果只安排生产书桌,最多可生产300张书桌,获得利润24000元
(2)设生产书桌x张,书橱y个,利润总额为z元.
则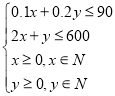 ,∴
,∴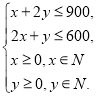
![]() 在直角坐标平面内作出上面不等式组所表示的平面区域,即可行域
在直角坐标平面内作出上面不等式组所表示的平面区域,即可行域
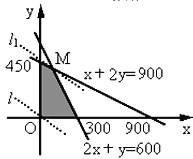
作直线![]() ,即直线
,即直线![]() .
.
把直线l向右上方平移至![]() 的位置时,直线经过可行域上的点M,
的位置时,直线经过可行域上的点M,
此时![]() 取得最大值
取得最大值
由![]() 解得点M的坐标为
解得点M的坐标为![]() .
.
∴当![]() ,
,![]() 时,
时,![]() (元).
(元).
因此,生产书桌100张、书橱400个,可使所得利润最大
所以当![]() ,
,![]() 时,
时,![]() .
.
因此,生产书桌100张、书橱400个,可使所得利润最大.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
【题目】如图![]() ,在高为
,在高为![]() 的等腰梯形
的等腰梯形![]() 中,
中,![]() ,且
,且![]() ,
,![]() ,将它沿对称轴
,将它沿对称轴![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,如图
,如图![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上(不同于
上(不同于![]() ,
,![]() 两点),连接
两点),连接![]() 并延长至点
并延长至点![]() ,使
,使![]() .
.
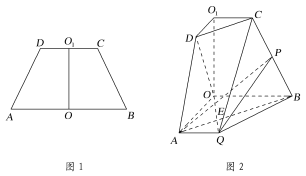
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,
中,![]() 是过定点
是过定点![]() 且倾斜角为
且倾斜角为![]() 的直线;在极坐标系(以坐标原点
的直线;在极坐标系(以坐标原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴,取相同单位长度)中,曲线
轴非负半轴为极轴,取相同单位长度)中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的参数方程,并将曲线
的参数方程,并将曲线![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)若曲线![]() 与直线
与直线![]() 相交于不同的两点
相交于不同的两点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
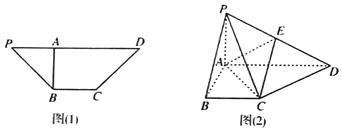
【题目】如图![]() 在四边形PBCD中,
在四边形PBCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,沿AB把三角形PAB折起,使P,D两点的距离为10,得到如图
,沿AB把三角形PAB折起,使P,D两点的距离为10,得到如图![]() 所示图形.
所示图形.
![]() Ⅰ
Ⅰ![]() 求证:平面
求证:平面![]() 平面PAC;
平面PAC;
![]() Ⅱ
Ⅱ![]() 若点E是PD的中点,求三棱锥
若点E是PD的中点,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有长分别为![]() 、
、![]() 、
、![]() 的钢管各3根(每根钢管的质地均匀、粗细相同且富有不同的编号),从中随机抽取
的钢管各3根(每根钢管的质地均匀、粗细相同且富有不同的编号),从中随机抽取![]() 根(假设各钢管被抽取的可能性是均等的,
根(假设各钢管被抽取的可能性是均等的,![]() ),再将抽取的钢管相接焊成笔直的一根.
),再将抽取的钢管相接焊成笔直的一根.
(I)当![]() 时,记事件
时,记事件![]() ,求
,求![]() ;
;
(II)当![]() 时,若用
时,若用![]() 表示新焊成的钢管的长度(焊接误差不计),求
表示新焊成的钢管的长度(焊接误差不计),求![]() 的分布列和数学期望
的分布列和数学期望![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C的方程为
中,曲线C的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线C的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与
与![]() 轴和y轴分别交于A,B两点,P为曲线C上的动点,求△PAB面积的最大值.
轴和y轴分别交于A,B两点,P为曲线C上的动点,求△PAB面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com