
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 ①两边都除以ab,得到答案;②利用基本不等式的性质得到答案;③作差法证明即可;④通过对数函数的性质判断即可.
解答 解:若a>b≥2,
对于①:不等式两边都除以ab得:$\frac{1}{a}$<$\frac{1}{b}$,故①正确;
对于②:根据基本不等式的性质得:a+b>2$\sqrt{ab}$,故②正确;
对于③:ab-(a+b )=$\frac{ab-2a+ab-2b}{2}$=$\frac{a(b-2)+b(a-2)}{2}$>$\frac{0+0}{2}$=0,故③正确;
对于④:不正确,如a=9,b=3 时,左边为$\frac{1}{2}$,右边为1,显然不等式不成立.
综上,只有①②③正确,
故选:D.
点评 本题考查了基本不等式的性质,考查对数函数的性质,是一道基础题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\stackrel{∧}{y}$=-2x+9.5 | B. | $\stackrel{∧}{y}$=-0.3x+4.2 | C. | $\stackrel{∧}{y}$=0.4x+2.3 | D. | $\stackrel{∧}{y}$=2x-2.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
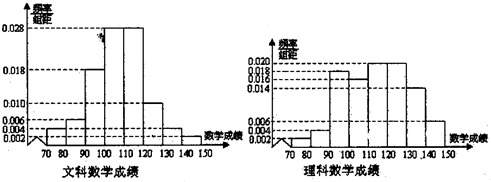
| 文科 | 理科 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 | 50 | 50 | 100 |
| P(K2>k) | 0.10 | 0.025 | 0.010 |
| K2 | 2.706 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com