
【题目】已知![]() ,又
,又![]() 有四个零点,则实数
有四个零点,则实数![]() 的取值范围是( )
的取值范围是( )
A.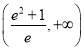 B.
B.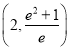 C.
C.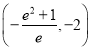 D.
D.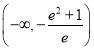
【答案】A
【解析】
由题意首先将函数写成分段函数的形式研究函数![]() 的性质,然后结合二次函数的性质研究复合函数
的性质,然后结合二次函数的性质研究复合函数![]() 的性质即可确定实数
的性质即可确定实数![]() 的取值范围.
的取值范围.
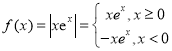 ,
,
当x0时,![]() 恒成立,所以f(x)在[0,+∞)上为增函数;
恒成立,所以f(x)在[0,+∞)上为增函数;
当x<0时,![]() ,
,
由f′(x)=0,得x=1,当x∈(∞,1)时,f′(x)=ex(x+1)>0,f(x)为增函数,
当x∈(1,0)时,f′(x)=ex(x+1)<0,f(x)为减函数,
所以函数f(x)=|xex|在(∞,0)上有一个最大值为![]() ,
,
则函数![]() 的大致图象如图所示:
的大致图象如图所示:
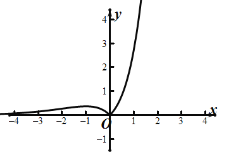
令f(x)=m,要使方程f2(x)tf(x)+1=0(t∈R)有四个实数根,
则方程m2-tm+1=0应有两个不等根,且一个根在![]() 内,一个根在
内,一个根在![]() 内.
内.
再令h(m)=m2m+1,因为h(0)=1>0,则只需![]() ,即
,即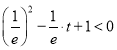 ,解得
,解得![]() .
.
故选:A.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为R,且
的定义域为R,且![]() 的图像过点
的图像过点![]() .
.
(1)求实数b的值;
(2)若函数![]() 在
在![]() 上单调递增,求实数a的取值范围;
上单调递增,求实数a的取值范围;
(3)是否存在实数a,使函数![]() 在R上的最大值为
在R上的最大值为![]() ?若存在,求出a的值;若不存在,请说明理由?
?若存在,求出a的值;若不存在,请说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国自改革开放以来,生活越来越好,肥胖问题也目渐显著,为分析肥胖程度对总胆固醇与空腹血糖的影响,在肥胖人群中随机抽出8人,他们的肥胖指数![]() 值、总胆固醇
值、总胆固醇![]() 指标值单位:
指标值单位: ![]() )、空腹血糖
)、空腹血糖![]() 指标值(单位:
指标值(单位: ![]() )如下表所示:
)如下表所示:

(1)用变量![]() 与
与![]() 与
与![]() 的相关系数,分别说明
的相关系数,分别说明![]() 指标值与
指标值与![]() 值、
值、![]() 指标值与
指标值与![]() 值的相关程度;
值的相关程度;
(2)求![]() 与
与![]() 的线性回归方程,已知
的线性回归方程,已知![]() 指标值超过5.2为总胆固醇偏高,据此模型分析当
指标值超过5.2为总胆固醇偏高,据此模型分析当![]() 值达到多大时,需要注意监控总胆固醇偏高情况的出现(上述数据均要精确到0.01)
值达到多大时,需要注意监控总胆固醇偏高情况的出现(上述数据均要精确到0.01)
参考公式:相关系数
 ,
,  ,
,![]() .
.
参考数据: ![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (k
(k![]() R),且满足f(﹣1)=f(1).
R),且满足f(﹣1)=f(1).
(1)求k的值;
(2)若函数y=f(x)的图象与直线![]() 没有交点,求a的取值范围;
没有交点,求a的取值范围;
(3)若函数![]() ,x
,x![]() [0,log23],是否存在实数m使得h(x)最小值为0,若存在,求出m的值;若不存在,请说明理由.
[0,log23],是否存在实数m使得h(x)最小值为0,若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为 ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 与曲线
与曲线![]() 两交点所在直线的极坐标方程;
两交点所在直线的极坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() (其中第一项是
(其中第一项是![]() ,接下来的
,接下来的![]() 项是
项是![]() ,再接下来的
,再接下来的![]() 项是
项是![]() ,依此类推)的前
,依此类推)的前![]() 项和为
项和为![]() ,下列判断:
,下列判断:
①![]() 是
是![]() 的第
的第![]() 项;②存在常数
项;②存在常数![]() ,使得
,使得![]() 恒成立;③
恒成立;③![]() ;④满足不等式
;④满足不等式![]() 的正整数
的正整数![]() 的最小值是
的最小值是![]() .
.
其中正确的序号是( )
A.①③B.①④C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程:
的参数方程: ![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程:
的参数方程:  (
(![]() 为参数),且直线交曲线
为参数),且直线交曲线![]() 于
于![]() 两点.
两点.
(1)将曲线![]() 的参数方程化为普通方程,并求
的参数方程化为普通方程,并求![]() 时,
时, ![]() 的长度;
的长度;
(2)巳知点![]() ,求当直线倾斜角
,求当直线倾斜角![]() 变化时,
变化时, ![]() 的范围.
的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com