
设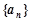 是有穷数列,且项数
是有穷数列,且项数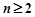 .定义一个变换
.定义一个变换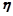 :将数列
:将数列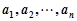 ,变成
,变成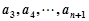 ,其中
,其中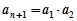 是变换所产生的一项.从数列
是变换所产生的一项.从数列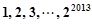 开始,反复实施变换
开始,反复实施变换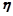 ,直到只剩下一项而不能变换为止.则变换所产生的所有项的乘积为
,直到只剩下一项而不能变换为止.则变换所产生的所有项的乘积为
A.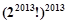 | B.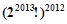 | C.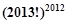 | D.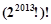 |
科目:高中数学 来源: 题型:单选题
若称 为n个正数a1+a2+…+an的“均倒数”已知数列{an}的各项均为正,且其前n项的“均倒数”为
为n个正数a1+a2+…+an的“均倒数”已知数列{an}的各项均为正,且其前n项的“均倒数”为 则数列{an}的通项公式为
则数列{an}的通项公式为
A.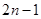 | B.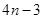 | C.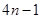 | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知定义在R上的函数f(x),g(x)满足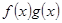 =ax,且f′(x)g(x)+f(x)·g′(x)<0,
=ax,且f′(x)g(x)+f(x)·g′(x)<0,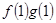 +
+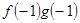 =
=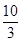 ,若有穷数列{
,若有穷数列{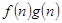 }(n∈N*)的前n项和等于
}(n∈N*)的前n项和等于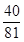 ,则n等于 .
,则n等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com