Question

20．已知点A（5，0），抛物线C：y²=8x的焦点为F，点P在抛物线C上，若点F恰好在PA的垂直平分线上，则PA的长度为2$\sqrt{6}$．

Answer 1

分析 利用已知条件，判断三角形PFA的形状，利用抛物线的性质与抛物线方程求出P的坐标，通过两点间距离公式求解即可．

解答 解：点A（5，0）在x轴上，抛物线C：y²=8x的焦点为F（2，0），
点P在抛物线C上，若点F恰好在PA的垂直平分线上，
可知三角形PFA是等腰三角形，即：|PF|=|AF|，可得|PF|=3，
由抛物线的定义可知，丨PF丨=x+$\frac{p}{2}$=3，则x=1，当x=1时，y=2$\sqrt{2}$，
∴P（1，2$\sqrt{2}$）．
则丨PA丨=$\sqrt{（1-5）^{2}+（2\sqrt{2}）^{2}}$=2$\sqrt{6}$．
故答案为：2$\sqrt{6}$．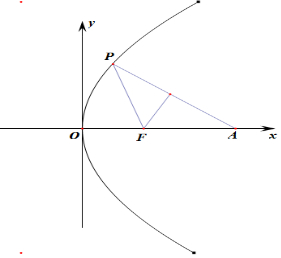

点评 本题考查直线与抛物线的位置关系的应用，抛物线的简单性质的应用，考查计算能力，属于中档题．