
分析 (1)设P(m,$\frac{1}{m}$),求出函数的导数,可得切线的斜率,运用点斜式方程求得切线的方程,分别令x=0,y=0,可得Q,R的坐标,再由中点坐标公式即可得证;
(2)运用三角形的面积公式可得S=$\frac{1}{2}$|OQ|•|OR|,计算即可得证.
解答 证明:(1)设P(m,$\frac{1}{m}$),由y=$\frac{1}{x}$可得y′=-$\frac{1}{{x}^{2}}$,
即有P点出的切线的斜率为-$\frac{1}{{m}^{2}}$,
切线的方程为y-$\frac{1}{m}$=-$\frac{1}{{m}^{2}}$(x-m),
由x=0,可得y=$\frac{2}{m}$;y=0可得x=2m.
即有Q(2m,0),R(0,$\frac{2}{m}$),
则P为QR的中点,即P平分QR;
(2)△OQR的面积是S=$\frac{1}{2}$|OQ|•|OR|
=$\frac{1}{2}$•2|m|•$\frac{2}{|m|}$=2为定值.
点评 本题考查导数的运用:求切线的方程,注意运用导数的几何意义和直线的方程,考查中点坐标公式和三角形的面积计算,属于中档题.


科目:高中数学 来源: 题型:解答题
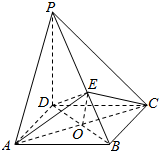 如图所示,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=$\sqrt{6}$.O为AC与BD的交点,E为棱PB上一点
如图所示,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=$\sqrt{6}$.O为AC与BD的交点,E为棱PB上一点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | “0<x<$\frac{1}{2}$”是“x(1-2x)>0”的必要不充分条件 | |
| C. | 命题“?x0∈R,使得x02+x0+1<0”的否定是:“?x∈R,均有x2+x+1>0” | |
| D. | 命题“在△ABC中,若A>B,则sinA>sinB”的逆否命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)<f(b) | B. | f(a)>f(b) | C. | f(a)>f(e) | D. | f(e)>f(b) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 雄蟹 | 雌蟹 | |||||
| 等级 | 特级 | 一级 | 二级 | 特级 | 一级 | 二级 |
| 只数 | 30 | a | 10 | 20 | 10 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com