
分析 由题意化简f(f(x))-x=[f(x)-x][af(x)+ax+b+1],从而化为解方程a2x2+(ab+a)x+ac+b+1=0;再由判别式判断即可.
解答 解:f(f(x))=x没有实数根,证明如下,
f(f(x))-x=af2(x)+bf(x)+c-x
=af2(x)-axf(x)+axf(x)-ax2+bf(x)-bx+ax2+bx+c-x
=af(x)[f(x)-x)]+ax[f(x)-x]+b[f(x)-x]+f(x)-x
=[f(x)-x][af(x)+ax+b+1]=0,
∵f(x)=x没有实数根,
∴△=(b-1)2-4ac<0,
且af(x)+ax+b+1=0;
即a(ax2+bx+c)+ax+b+1=0
a2x2+(ab+a)x+ac+b+1=0
△=(ab+a)2-4a2(ac+b+1)=a2[(b-1)2-4ac-4]<-4a2<0,
∴f[f(x)]=x一定没有实数根.
点评 本题考查了方程的根与复合函数的应用,同时考查了复合函数的化简与因式分解的应用,化简比较困难,属于中档题.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
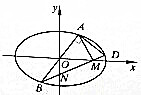 对于椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),c为椭圆半焦距,e为椭圆离心率,过原点O的直线与椭圆C交于A、B两点(A、B不是椭圆C的顶点),点D在椭圆C上,且AD⊥AB,直线BD与x轴、y轴分别交于M、N两点,证明:
对于椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),c为椭圆半焦距,e为椭圆离心率,过原点O的直线与椭圆C交于A、B两点(A、B不是椭圆C的顶点),点D在椭圆C上,且AD⊥AB,直线BD与x轴、y轴分别交于M、N两点,证明:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com