Question

12．如图，正方体ABCD-A₁B₁C₁D₁，下列四个结论：
（1）AC₁⊥BD；（2）BD∥平面CB₁D₁；（3）AC₁⊥平面CB₁D₁
（4）异面直线AD，CB₁所成角为$\frac{π}{3}$，其中正确命题的序号有（1）（2）（3）．

Answer 1

分析 根据线面垂直的判定定理，线面垂直的性质，线面平行的判定定理，以及异面直线所成角的概念及其求法即可判断每个命题的真假，从而得出正确答案．

解答 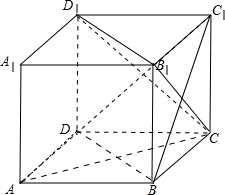解：如图，
（1）连接AC，∵CC₁⊥底面ABCD，BD?底面ABCD；
∴CC₁⊥BD，即BD⊥CC₁；
又BD⊥AC，AC∩CC₁=C；
∴BD⊥平面ACC₁；
∴BD⊥AC₁；
∴该命题正确；
（2）∵BD∥B₁D₁，B₁D₁?平面CB₁D₁，BD?平面CB₁D₁；
∴BD∥平面CB₁D₁；
∴该命题正确；
（3）连接BC₁，则B₁C⊥BC₁；
又AB⊥B₁C，即B₁C⊥AB，AB∩BC₁=B；
∴B₁C⊥平面ABC₁；
∴AC₁⊥B₁C；
又B₁D₁∥BD，AC₁⊥BD；
∴AC₁⊥B₁D₁，B₁D₁∩B₁C=B₁；
∴AC₁⊥平面CB₁D₁；
∴该命题正确；
（4）∵BC∥AD；
∴$∠{B}_{1}CB=\frac{π}{4}$为异面直线AD，CB₁所成角；
∴该命题错误；
∴正确命题的序号为：（1）（2）（3）．

点评 考查线面垂直的判定定理及其性质，线面平行的判定定理，以及异面直线所成角的概念及其求法．