
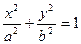 (a>b>0)的离心率为
(a>b>0)的离心率为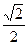 ,长轴长为
,长轴长为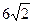 ,设过右焦点F倾
,设过右焦点F倾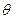 的直线交椭圆M于A,B两点。
的直线交椭圆M于A,B两点。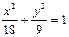 ,
,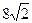
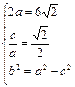
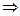
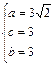 所求椭圆M的方程为
所求椭圆M的方程为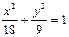 …3分
…3分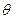 ≠
≠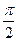 ,设直线AB的斜率为k = tan
,设直线AB的斜率为k = tan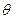 ,焦点F ( 3 , 0 ),则直线AB的方程为 y = k ( x – 3 ) 有
,焦点F ( 3 , 0 ),则直线AB的方程为 y = k ( x – 3 ) 有
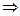 ( 1 + 2k2 )x2 – 12k2x + 18( k2 – 1 ) =" 0"
( 1 + 2k2 )x2 – 12k2x + 18( k2 – 1 ) =" 0" 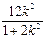 , x1x2 =
, x1x2 =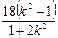
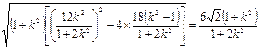
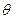 =
=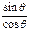 代入**式得 |AB| =
代入**式得 |AB| =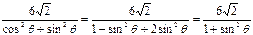
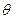 =
=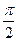 时,直线AB的方程为x = 3,此时|AB| =
时,直线AB的方程为x = 3,此时|AB| =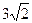
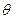 =
=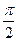 时,|AB| =
时,|AB| =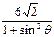 =
=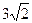
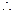 |AB| =
|AB| =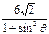
 =
=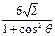
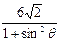 +
+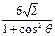 =
=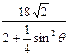
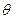 ∈[0,1],所以 当且仅当sin2
∈[0,1],所以 当且仅当sin2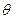 =1时,|AB|+|CD|有最小值是
=1时,|AB|+|CD|有最小值是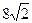


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 :
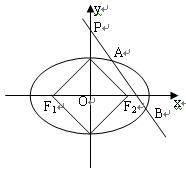
: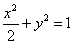 的左、右焦点分别为
的左、右焦点分别为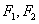 ,下顶点为
,下顶点为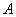 ,点
,点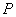 是椭圆上任一点,⊙
是椭圆上任一点,⊙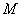 是以
是以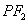 为直径的圆.
为直径的圆.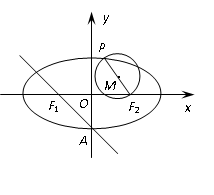
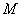 的面积为
的面积为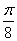 时,求
时,求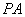 所在直线的方程;
所在直线的方程;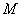 与直线
与直线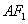 相切时,求⊙
相切时,求⊙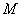 的方程;
的方程; 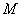 总与某个定圆相切.
总与某个定圆相切.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
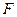 是椭圆
是椭圆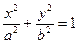 (a>b>0)的左焦点,直线
(a>b>0)的左焦点,直线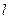 为对应的准线,直线
为对应的准线,直线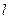 与
与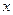 轴
轴 
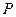 点,
点, 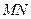 为椭圆的长轴,已知
为椭圆的长轴,已知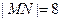 ,且
,且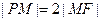 .
.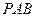 ,恒有
,恒有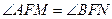 ;
;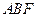 面积的最大值.
面积的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
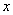 轴上,左右焦点分别为
轴上,左右焦点分别为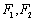 ,且
,且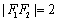 ,点(1,
,点(1,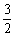 )在椭圆C上.
)在椭圆C上.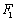 的直线
的直线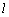 与椭圆
与椭圆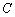 相交于
相交于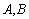 两点,且
两点,且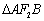 的面积为
的面积为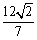 ,求以
,求以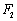 为圆心且与直线
为圆心且与直线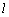 相切的圆的方程
相切的圆的方程查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
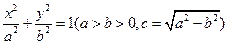 ,定义
,定义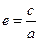 为椭圆的离心率,椭圆离心率的取值范围是
为椭圆的离心率,椭圆离心率的取值范围是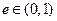 ,离心率越大椭圆越“扁”,离心率越小则椭圆越“圆”.若两椭圆的离心率相等,我们称两椭圆相似.已知椭圆
,离心率越大椭圆越“扁”,离心率越小则椭圆越“圆”.若两椭圆的离心率相等,我们称两椭圆相似.已知椭圆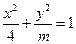 与椭圆
与椭圆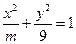 相似,则
相似,则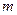 的值为
的值为 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com