考点:双曲线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:连接OM,AF2,过A作AN⊥x轴,垂足为N,求出抛物线方程和准线方程,由直线和圆相切的条件可得|OM|=a,
再由中位线定理可得|AF2|=2a,结合抛物线的定义可得A的坐标,过A作AH⊥l,垂足为H,求出|HF1|,即可得到4b2-4a2=4c(2a-c),再由a,b,c的关系及离心率公式计算即可得到.
解答:
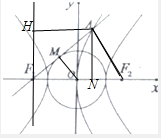
解:连接OM,AF
2,过A作AN⊥x轴,垂足为N,
由于F
1(-c,0),F
2(c,0),
则抛物线的方程为y
2=4cx,准线方程为x=-c,
作出准线l,过A作AH⊥l,垂足为H,
则有|AN|=|HF
1|,
由直线AF
1与圆x
2+y
2=a
2相切于点M,则|OM|=a,
由OM为三角形AF
1F
2的中位线,可得|AF
2|=2|OM|=2a,
由抛物线的定义可得|AF
2|=|AH|=x
A+c,即x
A=2a-c,
即有y
A=
,
又|MF|=
=b,则|AF
1|=2b,
在直角△HAF
1中,|HF
1|=
=
,
即有4b
2-4a
2=4c(2a-c),
即c
2-a
2-a
2=2ac-c
2,
即有c
2-a
2-ac=0,
由e=
,即有e
2-e-1=0,
由于e>1,解得e=
.
故选:A.
点评:本题考查双曲线的方程和性质,主要考查抛物线的定义、方程和性质,考查直线和圆相切的条件,运用三角形的中位线定理和勾股定理是解题的关键.

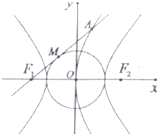 如图,双曲线C1:
如图,双曲线C1: 解:连接OM,AF2,过A作AN⊥x轴,垂足为N,
解:连接OM,AF2,过A作AN⊥x轴,垂足为N,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案