练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．六名大四学生（其中4名男生、2名女生）被安排到A、B、C三所学校实习，每所学校2人，且2名女生不到同一学校，也不到C学校，男生甲不到A学校，则不同的安排方法共有（　　）
    A．24B．36C．16D．18

    分析 根据题意，分4步进行分析：①、2名女生在A、B学校个一人，②、A学校除男生甲之外选男生一人，③、B学校在剩余男生中选一人，④、C学校2名男生，分别求出每一步的情况数目，由分步计数原理计算可得答案．

    解答 解：根据题意，要求六名学生被安排到A、B、C三所学校实习，每所学校2人，且2名女生不到同一学校，也不到C学校，男生甲不到A学校，
    只能安排2名女生在A、B学校各一人，有A22=2种安排方法，
    A学校除男生甲之外选男生一人，有C31=3种安排方法，
    B学校在剩余男生中选一人，有C31=3种安排方法，
    C学校选剩余的2名男生，有1种情况，
    则不同的安排方法有2×3×3×1=18种安排方法；
    故选：D．

    点评 本题考查排列、组合的综合应用，注意分析题目中的限制条件，注意受到限制的元素的处理方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．在△ABC中，tanC=2，BC边上的高为AD，D为垂足，且BD=2DC，则cosA=（　　）
    A．$\frac{3}{10}$B．$\frac{\sqrt{10}}{10}$C．$\frac{\sqrt{5}}{5}$D．$\frac{3\sqrt{10}}{10}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

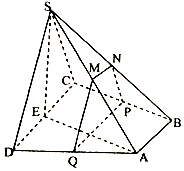    13．如图，四棱锥S-ABCD中，底面ABCD为直角梯形，AB∥CD，BC⊥CD，平面SCD⊥平面ABCD，SC=SD=CD=AD=2AB，M，N分别为SA，SB的中点，E为CD中点，过M，N作平面MNPQ分别与BC，AD交于点P，Q，若$\overrightarrow{DQ}$=t$\overrightarrow{DA}$．
    （1）当t=$\frac{1}{2}$时，求证：平面SAE⊥平面MNPQ；
    （2）是否存在实数t，使得二面角M-PQ-A的平面角的余弦值为$\frac{\sqrt{5}}{5}$？若存在，求出实数t的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知向量$\overrightarrow{AB}$、$\overrightarrow{AC}$、$\overrightarrow{AD}$满足$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$，|$\overrightarrow{AB}$|=2，|$\overrightarrow{AD}$|=1，E、F分别是线段BC、CD的中点，若$\overrightarrow{DE}$•$\overrightarrow{BF}$=-$\frac{5}{4}$，则向量$\overrightarrow{AB}$与$\overrightarrow{AD}$的夹角为（　　）
    A．$\frac{π}{6}$B．$\frac{π}{3}$C．$\frac{2π}{3}$D．$\frac{5π}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．如果正整数M的各位数字均不为4，且各位数字之和为6，则称M为“幸运数”，则四 位正整数中的“幸运数”共有（　　）
    A．45个B．41个C．40个D．38个

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．过抛物线C：y2=2px（p＞0）的焦点F的直线l与抛物线交于M，N两点，若$\overrightarrow{MF}$=4$\overrightarrow{FN}$，则直线l的斜率为（　　）
    A．±$\frac{3}{2}$B．±$\frac{2}{3}$C．±$\frac{3}{4}$D．±$\frac{4}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知α=sin150°，b=tan60°，c=cos（-120°），则a、b、c的大小关系是（　　）
    A．a＞b＞cB．b＞a＞cC．a＞c＞bD．b＞c＞a

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点F（-c，0）（c＞0），作倾斜角为$\frac{π}{6}$的直线FE交该双曲线右支于点P，若$\overrightarrow{OE}$=$\frac{1}{2}$（$\overrightarrow{OF}$+$\overrightarrow{OP}$），且$\overrightarrow{OE}$•$\overrightarrow{EF}$=0，则双曲线的离心率为（　　）
    A．$\frac{\sqrt{10}}{5}$B．$\sqrt{3}$+1C．$\frac{\sqrt{10}}{2}$D．$\sqrt{5}$+1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．若抛物线y2=8x的准线和圆x2+y2+6x+m=0相切，则实数m的值是8．

    查看答案和解析>>

    同步练习册答案