
已知椭圆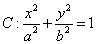
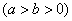 的离心率为
的离心率为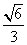 ,长轴长为
,长轴长为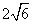 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设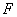 为椭圆C的右焦点,T为直线
为椭圆C的右焦点,T为直线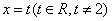 上纵坐标不为
上纵坐标不为 的任意一点,过
的任意一点,过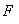 作
作 的垂线交椭圆C于点P,Q.
的垂线交椭圆C于点P,Q.
(ⅰ)若OT平分线段PQ(其中O为坐标原点),求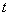 的值;
的值;
(ⅱ)在(ⅰ)的条件下,当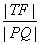 最小时,求点T的坐标.
最小时,求点T的坐标.
.解:(1)由已知解得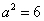
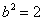
所以椭圆C的标准方程是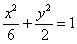 . ………………………………(3分)
. ………………………………(3分)
(2)(ⅰ)由(1)可得,F点的坐标是(2,0).
设直线PQ的方程为x=my+2,将直线PQ的方程与椭圆C的方程联立,得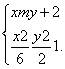
消去x,得(m2+3)y2+4my-2=0,其判别式Δ=16m2+8(m2+3)>0.
设P(x1,y1),Q(x2,y2),则y1+y2=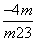 ,y1y2=
,y1y2=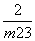 .于是x1+x2=m(y1+y2)+4=
.于是x1+x2=m(y1+y2)+4=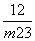 .
.
设M为PQ的中点,则M点的坐标为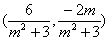 . …………6分
. …………6分
因为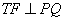 ,所以直线FT的斜率为
,所以直线FT的斜率为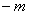 ,其方程为
,其方程为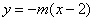 .
.
当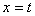 时,
时, ,所以点
,所以点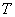 的坐标为
的坐标为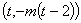 ,
,
此时直线OT的斜率为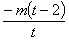 ,其方程为
,其方程为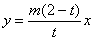 .
.
将M点的坐标为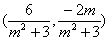 代入,得
代入,得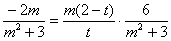 .
.
解得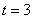 . ………………………………………………8分
. ………………………………………………8分
(ⅱ)由(ⅰ)知T为直线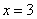 上任意一点可得,点T点的坐标为
上任意一点可得,点T点的坐标为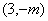 .
.
于是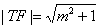 ,
, 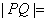
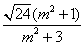 . …………10分
. …………10分
所以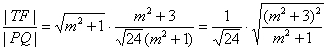
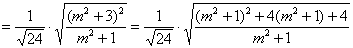
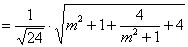
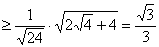 . ……………12分
. ……………12分
当且仅当m2+1=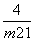 ,即m=±1时,等号成立,此时
,即m=±1时,等号成立,此时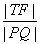 取得最小值
取得最小值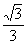 .
.
故当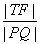 最小时,T点的坐标是(3,1)或(3,-1). ……………12分
最小时,T点的坐标是(3,1)或(3,-1). ……………12分


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
运货卡车以每小时x千米的速度匀速行驶130千米(50≤x≤100)(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油(2+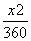 )升,司机的工资是每小时14元.
)升,司机的工资是每小时14元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
设圆(x+1)2+y2=25的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点,线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( )
A.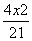 -
-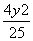 =1 B.
=1 B.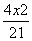 +
+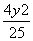 =1 C.
=1 C.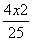 -
-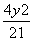 =1 D.
=1 D.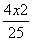 +
+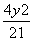 =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
三段论:“①小宏在2013年的高考中考入了重点本科院校;②小宏在2013年的高考中只要正常发挥就能考入重点本科院校;③小宏在2013年的高考中正常发挥”中,“小前提”是__________(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com