
���� ��������������a=2c����Բ����Ϊֱ����Բ��Բ�ĵ�ֱ��y=x+1����d=$\frac{1}{{\sqrt{2}}}$�������a��c�����p��
���ɵõ���ԲC�ķ��̣�������D���̣�
������A��x1��y1����B��x2��y2������ֱ��AB��x�ᴹֱʱ����AB��x=m����$y=��\frac{{\sqrt{12-3{m^2}}}}{2}$������OA��OB�����m���Ƴ�ԭ�㵽ֱ��AB�ľ��룮��ֱ��ABб�ʴ���ʱ����ֱ��AB�ķ���Ϊy=kx+m����3x2+4y2-12=0������Τ�ﶨ���Լ��б�ʽ����0����������������Ϊ0����⼴�ɣ�
��� �⣺��������֪$\frac{c}{a}$=$\frac{1}{2}$����a=2c����Բ����Ϊֱ����Բ��Բ�ĵ�ֱ��y=x+1����d=$\frac{1}{{\sqrt{2}}}$��
��$\sqrt{10}$=$2\sqrt{{b^2}-\frac{1}{2}}$�����b=$\sqrt{3}$����a2=$3+\frac{a^2}{4}$�����a2=4����c=1����$\frac{p}{2}$=1����p=2��
����ԲC�ķ���Ϊ$\frac{x^2}{4}+\frac{y^2}{3}=1$��������D����Ϊy2=4x�� 5��
������A��x1��y1����B��x2��y2������ֱ��AB��x�ᴹֱʱ����AB��x=m����$y=��\frac{{\sqrt{12-3{m^2}}}}{2}$��
��OA��OB����$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=${m^2}-\frac{{12-3{m^2}}}{4}$=0�����m=$��\frac{{2\sqrt{21}}}{7}$��
��ԭ�㵽ֱ��AB�ľ���Ϊ$\frac{{2\sqrt{21}}}{7}$�� 7�֣�
��ֱ��ABб�ʴ���ʱ����ֱ��AB�ķ���Ϊy=kx+m����3x2+4y2-12=0�����ã���3+4k2��x2+8kmx+4m2-12=0��
���=��8km��2-4��3+4k2����4m2-12����0����4k2-m2+3��0��x1+x2=$-\frac{8km}{{3+4{k^2}}}$��x1x2=$\frac{{4{m^2}-12}}{{3+4{k^2}}}$��
��y1y2=��kx1+m����kx2+m��=${k^2}{x_1}{x_2}+km��{x_1}+{x_2}��+{m^2}$=$\frac{{3{m^2}-12{k^2}}}{{3+4{k^2}}}$��
��OA��OB����$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=$\frac{{4{m^2}-12}}{{3+4{k^2}}}$+$\frac{{3{m^2}-12{k^2}}}{{3+4{k^2}}}$=0����7m2=12��k2+1����
���������0��10��
��ԭ�㵽ֱ��AB�ľ���Ϊ$\frac{|m|}{{\sqrt{1+{k^2}}}}$=$\frac{{2\sqrt{21}}}{7}$��11��
��ԭ��O��ֱ��AB�ľ���Ϊ��ֵ����ֵΪ$\frac{{2\sqrt{21}}}{7}$�� 12�֣�
���� ���⿼�������������������ϵ���������Լ���Բ���̵��ۺ�Ӧ�ã�������������������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
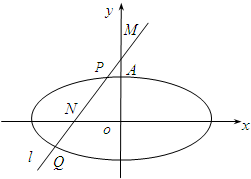 ��ͼ����֪��Բ������������ԭ�㣬������x���ϣ�����һ������ΪA��0��$\sqrt{2}$�����������ʵ���$\frac{{\sqrt{3}}}{2}$������M��0��2����ֱ��l����Բ�ཻ��P��Q��ͬ���㣬��N���߶�PQ�ϣ�
��ͼ����֪��Բ������������ԭ�㣬������x���ϣ�����һ������ΪA��0��$\sqrt{2}$�����������ʵ���$\frac{{\sqrt{3}}}{2}$������M��0��2����ֱ��l����Բ�ཻ��P��Q��ͬ���㣬��N���߶�PQ�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}+\frac{5}{2}i$ | B�� | $\frac{1}{2}-\frac{5}{2}i$ | C�� | $-\frac{1}{2}+\frac{5}{2}i$ | D�� | $-\frac{1}{2}-\frac{5}{2}i$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com