
分析 (1)将直线AB的方程代入椭圆方程,利用韦达定理及导数的几何意义,分别求得切线方程,联立即可求得点P的轨迹方程;
(2)分类讨论,根据直线斜率与倾斜角的关系,即可求得tanα取值范围,即可求得α的取值范围.
解答 解:(1)由AB直线与抛物线交于两点可知,直线AB不与x轴垂直,故可设lAB:y=kx+2,
则$\left\{\begin{array}{l}{{x}^{2}=4y}\\{y=kx+2}\end{array}\right.$,整理得:x2-4ky-8=0…①,
△=16k2+32>0,故k∈R时均满足题目要求.
设交点坐标为$A({x_1},\frac{{{x_1}^2}}{4}),B({x_2},\frac{{{x_2}^2}}{4})$,则x1,x2为方程①的两根,
故由韦达定理可知,x1+x2=4k,x1x2=-8.
将抛物线方程转化为$y=\frac{1}{4}{x^2}$,则$y'=\frac{1}{2}x$,故A点处的切线方程为$y-\frac{{{x_1}^2}}{4}=\frac{x_1}{2}(x-{x_1})$,
整理得$y=\frac{x_1}{2}x-\frac{{{x_1}^2}}{4}$,
同理可得,B点处的切线方程为$y=\frac{x_2}{2}x-\frac{{{x_2}^2}}{4}$,记两条切线的交点P(xp,yp),
联立两条切线的方程,解得点P坐标为${x_P}=\frac{{{x_1}+{x_2}}}{2}=2k,{y_P}=k{x_1}-\frac{{{x_1}^2}}{4}=k{x_1}-(k{x_1}+2)=-2$,
故点P的轨迹方程为y=-2,x∈R
(2)当k=0时,xP=0,yP=-2,此时直线PQ即为y轴,与直线AB的夹角为$\frac{π}{2}$.
当k≠0时,记直线PQ的斜率${k_{PQ}}=\frac{-2-2}{2k-0}=-\frac{2}{k}$,
又由于直线AB的斜率为k,且已知直线AB与直线PQ所夹角α∈[0,$\frac{π}{2}$],
tanα=丨$\frac{{k}_{PQ}-{k}_{AB}}{1+{k}_{PQ}•{k}_{AB}}$丨=丨$\frac{-\frac{2}{k}-k}{1-2}$丨=$\frac{2}{丨k丨}$+丨k丨≥2$\sqrt{2}$,
则a∈[arctan2$\sqrt{2}$,$\frac{π}{2}$)
综上所述,α的取值范围是∈[arctan2$\sqrt{2}$,$\frac{π}{2}$].
点评 本题考查直线与抛物线的位置关系,考查导数的几何意义,利用导数求切线方程,基本不等式的应用,考查计算能力,属于中档题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
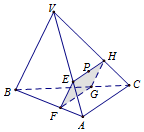 如图所示,在四面体VABC木块中,P为△VAC的重心,这点P作截面EFGH,若截面EFGH是平行四边形,则该截面把木块分成两部分体积之比为$\frac{7}{20}$. (埴体积小与体积大之比)
如图所示,在四面体VABC木块中,P为△VAC的重心,这点P作截面EFGH,若截面EFGH是平行四边形,则该截面把木块分成两部分体积之比为$\frac{7}{20}$. (埴体积小与体积大之比)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 81 47 23 68 63 93 17 90 12 69 86 81 62 93 50 60 91 33 75 85 61 39 85 |
| 06 32 35 92 46 22 54 10 02 78 49 82 18 86 70 48 05 46 88 15 19 20 49 |
| A. | 12 | B. | 33 | C. | 06 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $g(x)=sin(4x+\frac{π}{6})$ | B. | $g(x)=sin(4x-\frac{π}{3})$ | C. | $g(x)=sin(2x+\frac{π}{6})$ | D. | g(x)=sin2x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分又非必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com