

分析 (1)当a=90时,b=40,求出侧面积,利用配方法求纸盒侧面积的最大值;
(2)表示出体积,利用基本不等式,导数知识,即可确定a,b,x的值,使得纸盒的体积最大,并求出最大值.
解答 解:(1)因为矩形纸板ABCD的面积为3600,故当a=90时,b=40,
从而包装盒子的侧面积S=2×x(90-2x)+2×x(40-2x)=-8x2+260x,x∈(0,20).…(3分)
因为S=-8x2+260x=-8(x-16.25)2+2112.5,
故当x=16.25时,侧面积最大,最大值为2112.5平方厘米.
(2)包装盒子的体积V=(a-2x)(b-2x)x=x[ab-2(a+b)x+4x2],x∈(0,$\frac{b}{2}$),b≤60.…(8分)
V=x[ab-2(a+b)x+4x2]≤x(ab-4$\sqrt{ab}$x+4x2)=x(3600-240x+4x)
=4x3-240x2+3600x.…(10分)
当且仅当a=b=60时等号成立.
设f(x)=4x3-240x2+3600x,x∈(0,30).则f′(x)=12(x-10)(x-30).
于是当0<x<10时,f′(x)>0,所以f(x)在(0,10)上单调递增;
当10<x<30时,f′(x)<0,所以f(x)在(10,30)上单调递减.
因此当x=10时,f(x)有最大值f(10)=16000,…(12分)此时a=b=60,x=10.
答:当a=b=60,x=10时纸盒的体积最大,最大值为16000立方厘米.…(14分)
点评 本题考查导数知识的综合运用,考查基本不等式,考查利用数学知识解决实际问题的能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
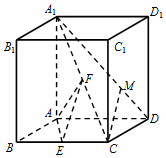 如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=$\frac{π}{3}$,E,F分别是BC,A1C的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=$\frac{π}{3}$,E,F分别是BC,A1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
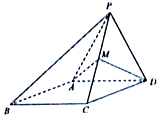 如图,四棱锥P-ABCD中,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ABC=60°,M为PC的中点.
如图,四棱锥P-ABCD中,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ABC=60°,M为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{9}-\frac{{y}^{2}}{27}=1$ | B. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{10}$-$\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{9}$=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com