考点:数列的求和
专题:等差数列与等比数列
分析:(1)由题设得
=,从而得到
an=Sn-Sn-1=2n-1,由此能求出数列{a
n}的通项公式.
(2)(文)由
bn=n•2n,利用错位相减法能求出{b
n}的前n项和为T
n.
(理)
bn==,由此利用错位相减法能证明
Tn <2.
解答:
(1)解:由题设得
=,
∴
Sn+n+3=2n+1+1,
Sn=2n+1-n-2,
n≥2时,
an=Sn-Sn-1=2n-1,
当n=1时也满足,∴
an=2n-1.…(6分)
(2)(文)解:
bn=n•2n,设{b
n}的前n项和为T
n,
T
n=1×2+2×2
2+3×2
3+…+(n-1)×2
n-1+n×2
n,(1)
2T
n=1×2
2+2×2
3+3×2
4+…+(n-1)×2
n+n×2
n+1,(2)
(1)-(2),-T
n=1×2+2
2+2
3+…+2
n-n×2
n+1=
-n×2n+1=2
n+1-2-n×
2n+1 ,
∴
Tn =(n-1)•2n+1+2.…(13分)
(理)证明:
bn==,
Tn=+++…++,①
Tn =
+++…++,②
①-②,整理得
Tn =2-
-=2-
<2.…(13分)
点评:本题考查数列的通项公式的证明,考查数列的前n项和的求法,考查不等式的证明,解题时要认真审题,注意错位相减法的合理运用.



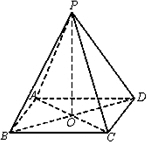 如图,在四棱锥P-ABCD中,底面ABCD是矩形,四条侧棱长均相等且BD交AC于点O.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,四条侧棱长均相等且BD交AC于点O. 如图,在三棱柱ABC-A1B1C1中,底面△ABC为直角三角形,∠ACB=
如图,在三棱柱ABC-A1B1C1中,底面△ABC为直角三角形,∠ACB=