
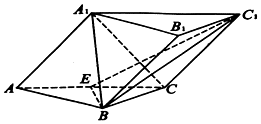
 如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥平面ABC,AB=BC=2,∠ACB=30°,∠C1CB=120°,BC1⊥A1C,E为AC的中点.
如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥平面ABC,AB=BC=2,∠ACB=30°,∠C1CB=120°,BC1⊥A1C,E为AC的中点.分析 (1)证明BE⊥平面A1ACC1,推出BE⊥A1C.BC1⊥A1C,证明A1C⊥面C1EB.
(2)方法一:作C1M⊥AC于M,作MN⊥BC于N,连C1N,通过cos∠C1CN=cos∠C1CM•cos∠NCM,求出$cos∠{C_1}CM=\frac{{\sqrt{3}}}{3}$.设AA1=x.设A1C与C1E交于点H,利用余弦定理以及勾股定理证明A1E⊥AC,过E作EF⊥AB于F,连A1F,说明∠A1FE为二面角A1-AB-C的平面角,然后求解即可.
方法二:以A点为原点,AC为y轴,过点A与平面ABC垂直的直线为z轴,建立如图所示的空间直角坐标系,设AA1=x,∠A1AC=θ,求出相关点的坐标,求出平面A1AB的法向量,平面ABC的法向量利用空间向量的数量积求解二面角A1-AB-C的余弦值.
解答 (1)证明:∵BA=BC,E为AC的中点,∴BE⊥AC,又平面A1ACC1⊥平面ABC,平面A1ACC1∩平面ABC=AC,BE?平面ABC,∴BE⊥平面A1ACC1,又A1C?平面A1ACC1,∴BE⊥A1C.
又BC1⊥A1C,BE∩BC1=B,∴A1C⊥面C1EB.
(2)解:方法一:由平面A1ACC1⊥平面ABC,作C1M⊥AC于M,则C1M⊥面ABC.
作MN⊥BC于N,连C1N,则C1N⊥BC,由$cos∠{C_1}CN=\frac{CN}{{C{C_1}}}$,$cos∠{C_1}CM=\frac{CM}{{C{C_1}}}$,$cos∠NCM=\frac{CN}{CM}$知cos∠C1CN=cos∠C1CM•cos∠NCM,而∠C1CM=60°,∠NCM=30°,故$\frac{1}{2}=cos∠{C_1}CM•\frac{{\sqrt{3}}}{2}$,即$cos∠{C_1}CM=\frac{{\sqrt{3}}}{3}$.
在四边形AA1C1C中,设AA1=x.
则由余弦定理得${A_1}{C^2}={x^2}+12-2x•2\sqrt{3}•\frac{{\sqrt{3}}}{3}={x^2}-4x+12$.${C_1}{E^2}={x^2}+3-2•x•\sqrt{3}•(-\frac{{\sqrt{3}}}{3})={x^2}+2x+3$,设A1C与C1E交于点H,则${A_1}H=\frac{2}{3}{A_1}C$,${C_1}H=\frac{2}{3}{C_1}E$,而A1C⊥C1E,则${A_1}{H^2}+{C_1}{H^2}={A_1}C_1^2$.
于是$\frac{4}{9}({x^2}-4x+12)+\frac{4}{9}({x^2}+2x+3)={(2\sqrt{3})^2}$,即x2-x-6=0,∴x=3或-2(舍)
容易求得:${A_1}E=\sqrt{6}$,而${A_1}{E^2}+A{E^2}=AA_1^2$.
故A1E⊥AC,由面A1ACC1⊥面ABC,则A1E⊥面ABC,过E作EF⊥AB于F,连A1F,则∠A1FE为二面角A1-AB-C的平面角,由平面几何知识易得$EF=\frac{{\sqrt{3}}}{2}$,${A_1}F=\frac{3}{2}\sqrt{3}$.
∴$cos∠{A_1}FE=\frac{AE}{{{A_1}F}}=\frac{{\frac{{\sqrt{3}}}{2}}}{{\frac{{3\sqrt{3}}}{2}}}=\frac{1}{3}$.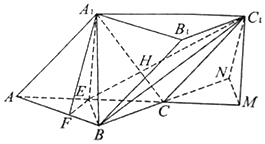
方法二:以A点为原点,AC为y轴,过点A与平面ABC垂直的直线为z轴,建立如图所示的空间直角坐标系,设AA1=x,∠A1AC=θ,则$B(1,\sqrt{3},0)$,$C(0,2\sqrt{3},0)$,$E(0,\sqrt{3},0)$,${C_1}(0,2\sqrt{3}+xcosθ,xsinθ)$.
∴$\overrightarrow{CB}=(1,-\sqrt{3},0)$,$\overrightarrow{C{C_1}}=(0,xcosθ,xsinθ)$.由$cos<\overrightarrow{CB},\overrightarrow{C{C_1}}>=\frac{{\overrightarrow{CB}•\overrightarrow{C{C_1}}}}{{|\overrightarrow{CB}||\overrightarrow{C{C_1}}|}}=-\frac{1}{2}$,得$\frac{{-\sqrt{3}x•cosθ}}{2x}=-\frac{1}{2}$,∴$cosθ=\frac{{\sqrt{3}}}{3}$,则${A_1}(0,\frac{{\sqrt{3}}}{3}x,\frac{{\sqrt{6}}}{3}x)$,${C_1}(0,2\sqrt{3}+\frac{{\sqrt{3}}}{3}x,\frac{{\sqrt{6}}}{3}x)$,于是$\overrightarrow{{A_1}C}=(0,2\sqrt{3}-\frac{{\sqrt{3}}}{3}x,-\frac{{\sqrt{6}}}{3}x)$,$\overrightarrow{B{C_1}}=(-1,\sqrt{3}+\frac{{\sqrt{3}}}{3}x,\frac{{\sqrt{6}}}{3})$,∵$\overrightarrow{{A_1}C}⊥\overrightarrow{B{C_1}}$,
∴$(\sqrt{3}+\frac{{\sqrt{3}}}{3}x)(2\sqrt{3}-\frac{{\sqrt{3}}}{3}x)-\frac{{\sqrt{6}}}{3}x•\frac{{\sqrt{6}}}{3}x=0$,即x2-x-6=0,解得x=3或-2(舍),故AA1=3,则${A_1}(0,\sqrt{3},\sqrt{6})$,$B(1,\sqrt{3},0)$,于是$\overrightarrow{A{A_1}}=(0,\sqrt{3},\sqrt{6})$,$\overrightarrow{AB}=(1,\sqrt{3},0)$,设平面A1AB的法向量为$\overrightarrow{n_1}=(x,y,z)$,则$\left\{\begin{array}{l}\overrightarrow{n_1}•\overrightarrow{A{A_1}}=0\\ \overrightarrow{n_1}•\overrightarrow{AB}=0\end{array}\right.$即$\left\{\begin{array}{l}\sqrt{3}y+\sqrt{6}z=0\\ x+\sqrt{3}y=0\end{array}\right.$,取y=1,则$z=-\frac{{\sqrt{2}}}{2},x=-\sqrt{3}$,∴$\overrightarrow{n_1}=(-\sqrt{3},1,-\frac{{\sqrt{2}}}{2})$.
不妨设平面ABC的法向量$\overrightarrow{n_2}=(0,0,1)$,则$cos<\overrightarrow{n_1},\overrightarrow{n_2}>=\frac{{\overrightarrow{n_1}•\overrightarrow{n_2}}}{{|\overrightarrow{n_1}||\overrightarrow{n_2}|}}=\frac{{\frac{{-\sqrt{2}}}{2}}}{{\sqrt{\frac{9}{2}}×1}}=-\frac{1}{3}$,
故二面角A1-AB-C的余弦值为$\frac{1}{3}$.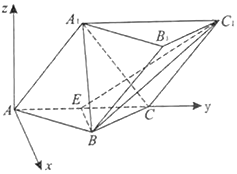
点评 本题考查直线与平面垂直的判定定理的应用,二面角的平面角的求法,空间向量数量积的应用,考查空间想象能力逻辑推理能力以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,2) | B. | (-2,4) | C. | (2,+∞) | D. | (-∞,-4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{8}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{{8\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{e}$ | B. | $\frac{1}{2e}$ | C. | $\frac{2}{e}$ | D. | $\frac{e}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com