
分析 (1)求出函数的导数,计算f′(e),求出a的值即可;
(2)求出$\frac{lnx}{x}-{x^2}+2ex=a$,记$F(x)=\frac{lnx}{x}-{x^2}+2ex$,根据函数的单调性求出F(x)的最大值,从而求出a的范围即可.
解答 解:(1)$f'(x)=\frac{1}{x}-3{x^2}+4ex-a$,
$f'(e)=\frac{1}{e}+{e^2}-a={e^2}$,∴$a=\frac{1}{e}$.
(2)由lnx-x3+2ex2-ax=0,
得$\frac{lnx}{x}-{x^2}+2ex=a$,
记$F(x)=\frac{lnx}{x}-{x^2}+2ex$,
则$F'(x)=\frac{1-lnx}{x}-2(x-e)$,x∈(e,+∞),
F'(x)<0,F(x)递减;
x∈(0,e)时,F'(x)>0,F(x)递增.
∴$F{(x)_{max}}=F(e)=\frac{1}{e}+{e^2}$.
而x→0时F(x)→-∞,
x→+∞时F(x)→-∞,
故$a<\frac{1}{e}+{e^2}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{6}$ | B. | 向右平移 $\frac{π}{6}$ | C. | 向左平移 $\frac{π}{3}$ | D. | 向右平移$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\sqrt{3}$ | C. | $-\sqrt{3}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
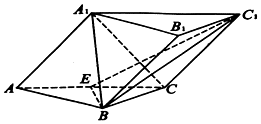 如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥平面ABC,AB=BC=2,∠ACB=30°,∠C1CB=120°,BC1⊥A1C,E为AC的中点.
如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥平面ABC,AB=BC=2,∠ACB=30°,∠C1CB=120°,BC1⊥A1C,E为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 广告费用x(万元) | 2 | 3 | 4 | 5 |
| 销售额y(万元) | 32 | 35 | 45 | 52 |
| A. | 58.5万元 | B. | 77.5万元 | C. | 59万元 | D. | 70万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-4,-2] | B. | [-4,+∞) | C. | [-3,+∞) | D. | [-3,-2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com