
| A. | (-2,3) | B. | (-2,4) | C. | (-1,4) | D. | (-1,3) |
分析 可作出图形,根据条件可以求出直线OB的方程,根据角平分线上的点到角的两边距离相等,从而去验证每个选项的点是否满足角平分线的性质即可找出正确选项.
解答 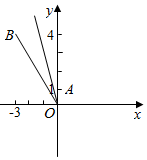 解:如图,直线OB的方程为$y=-\frac{4}{3}x$;
解:如图,直线OB的方程为$y=-\frac{4}{3}x$;
角平分线上的点到角两边的距离相等;
(-2,3)到OB的距离为$\frac{|\frac{8}{3}-3|}{\sqrt{1+\frac{16}{9}}}=\frac{1}{5}$,到y轴距离为2,∴C不可以为(-2,3);
(-2,4)到OB的距离为$\frac{4-\frac{8}{3}}{\frac{5}{3}}=\frac{4}{5}$,到y轴距离为2,∴C不可以为(-2,4);
(-1,4)到OB的距离为$\frac{4-\frac{4}{3}}{\frac{5}{3}}=\frac{8}{5}$,到y轴距离为1,∴C不可以为(-1,4);
(-1,3)到OB的距离为$\frac{3-\frac{4}{3}}{\frac{5}{3}}=1$,到y轴距离为1,∴C可以为(-1,3);
∴向量$\overrightarrow{OC}$可以等于(-1,3).
故选:D.
点评 考查根据直线上的点的坐标求过原点的直线斜率的计算公式,直线的点斜式方程,以及角平分线上的点到角的两边距离相等,点到直线的距离公式,也可根据作的图去判断.


科目:高中数学 来源: 题型:选择题
| A. | 任意两个一次函数最多存在一条“分界线” | |
| B. | “分界线”存在的两个函数的图象最多只有两个交点 | |
| C. | f(x)=x2-2x与g(x)=-x2+4的“分界线”是y=-x+2 | |
| D. | f(x)=x2与g(x)=-(x-1)2的“分界线”是y=0或$y=x-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
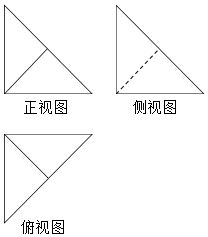 在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )
在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{\sqrt{2}}{4}$ | C. | 1 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com