
| A. | 2 | B. | $\frac{\sqrt{2}}{4}$ | C. | 1 | D. | 2$\sqrt{2}$ |
分析 令$\sqrt{4+t-2tx}$=m,则2x-1=$\frac{4-{m}^{2}}{t}$,从而利用配方法求最大值,再由基本不等式求最小值即可.
解答 解:令$\sqrt{4+t-2tx}$=m,则2x-1=$\frac{4-{m}^{2}}{t}$,
故f(x)=2x-1+$\sqrt{4+t-2tx}$
=$\frac{4-{m}^{2}}{t}$+m=$\frac{-(m-\frac{t}{2})^{2}+4+\frac{{t}^{2}}{4}}{t}$=F(m),
故g(t)=Fmax(m)=$\frac{4}{t}$+$\frac{t}{4}$≥2,
(当且仅当t=4时,等号成立),
故选A.
点评 本题考查了配方法的应用及基本不等式的应用,同时考查了换元法的应用.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 60°或120° | B. | 120° | C. | 60° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,3) | B. | (-2,4) | C. | (-1,4) | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
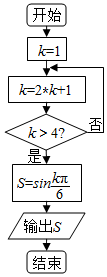
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
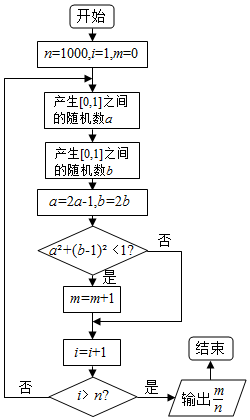
| A. | $\frac{π}{4}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com