
【题目】已知圆M的方程为x2+(y﹣2)2=1,直线l的方程为x﹣2y=0,点P在直线l上,过P点作圆M的切线PA,PB,切点为A,B.
(1)若∠APB=60°,试求点P的坐标;
(2)若P点的坐标为(2,1),过P作直线与圆M交于C,D两点,当 ![]() 时,求直线CD的方程;
时,求直线CD的方程;
(3)求证:经过A,P,M三点的圆必过定点,并求出所有定点的坐标.
【答案】
(1)解:设P(2m,m),由题可知MP=2,所以(2m)2+(m﹣2)2=4,
解之得: ![]() ,
,
故所求点P的坐标为P(0,0)或 ![]()
(2)解:设直线CD的方程为:y﹣1=k(x﹣2),易知k存在,
由题知圆心M到直线CD的距离为 ![]() ,所以
,所以 ![]() ,
,
解得,k=﹣1或 ![]() ,故所求直线CD的方程为:x+y﹣3=0或x+7y﹣9=0
,故所求直线CD的方程为:x+y﹣3=0或x+7y﹣9=0
(3)证明:设P(2m,m),MP的中点 ![]() ,
,
因为PA是圆M的切线,所以经过A,P,M三点的圆是以Q为圆心,以MQ为半径的圆,
故其方程为: ![]()
化简得:x2+y2﹣2y﹣m(2x+y﹣2)=0,此式是关于m的恒等式,
故x2+y2﹣2y=0且(2x+y﹣2)=0,
解得 ![]() 或
或 ![]()
所以经过A,P,M三点的圆必过定点(0,2)或( ![]() ,
, ![]() )
)
【解析】(1)设P(2m,m),代入圆方程,解得m,进而可知点P的坐标.(2)设直线CD的方程为:y﹣1=k(x﹣2),由圆心M到直线CD的距离求得k,则直线方程可得.(3)设P(2m,m),MP的中点 ![]() ,因为PA是圆M的切线,进而可知经过A,P,M三点的圆是以Q为圆心,以MQ为半径的圆,进而得到该圆的方程,根据其方程是关于m的恒等式,进而可求得x和y,得到经过A,P,M三点的圆必过定点的坐标.
,因为PA是圆M的切线,进而可知经过A,P,M三点的圆是以Q为圆心,以MQ为半径的圆,进而得到该圆的方程,根据其方程是关于m的恒等式,进而可求得x和y,得到经过A,P,M三点的圆必过定点的坐标.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】设集合A={x|0≤x≤2},B={y|1≤y≤2},若对于函数y=f(x),其定义域为A,值域为B,则这个函数的图象可能是( )
A.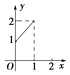
B.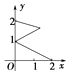
C.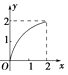
D.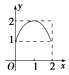
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC= ![]() AD=1,CD=
AD=1,CD= ![]() .
. 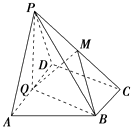
(1)求证:平面PQB⊥平面PAD;
(2)若二面角M﹣QB﹣C为30°,求线段PM与线段MC的比值t.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】x∈R,则f(x)与g(x)表示同一函数的是( )
A.f(x)=x2 , ![]()
B.f(x)=1,g(x)=(x﹣1)0
C.![]() ,
, ![]()
D.![]() ,g(x)=x﹣3
,g(x)=x﹣3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为抛物线E:y2=2px(p>0)的焦点,点A(3,m)在抛物线E上,且|AF|=4. 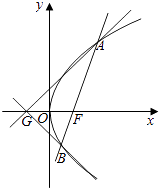
(1)求抛物线E的方程;
(2)已知点G(﹣1,0),延长AF交抛物线E于点B,证明:以点F为圆心且与直线GA相切的圆,必与直线GB相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,其中a>0.
,其中a>0.
(Ⅰ)当a=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求f(x)在区间[1,e]上的最小值.(其中e是自然对数的底数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com