
| A. | 4(4$\sqrt{2}$-$\sqrt{31}$) | B. | 4(4$\sqrt{2}$-$\sqrt{30}$) | C. | 4($\sqrt{33}$-4$\sqrt{2}$) | D. | 4($\sqrt{33}$-$\sqrt{31}$) |
分析 an+1=$\frac{n}{{S}_{n+1}+{S}_{n}}$(n∈N+),可得${S}_{n+1}^{2}$-${S}_{n}^{2}$=n,利用“累加求和”方法、等差数列的求和公式及其递推关系即可得出.
解答 解:∵an+1=$\frac{n}{{S}_{n+1}+{S}_{n}}$(n∈N+),an+1=Sn+1-Sn,∴${S}_{n+1}^{2}$-${S}_{n}^{2}$=n,
∴${S}_{n}^{2}$=$({S}_{n}^{2}$-${S}_{n-1}^{2})$+$({S}_{n-1}^{2}-{S}_{n-2}^{2})$+…+$({S}_{2}^{2}-{S}_{1}^{2})$+${S}_{1}^{2}$=(n-1)+(n-2)+…+1+0=$\frac{n(n-1)}{2}$.
∴Sn=$\sqrt{\frac{n(n-1)}{2}}$,
∴a33=S33-S32=$\sqrt{\frac{33×32}{2}}$-$\sqrt{\frac{32×31}{2}}$=4$(\sqrt{33}-\sqrt{31})$,
故选:D.
点评 本题考查了等差数列的通项公式与求和公式、“累加求和”方法、递推关系,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
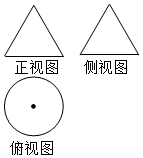 某几何体的三视图如图所示,其中正视图和俯视图都是腰长为2的等腰三角形,俯视图是半径为1的圆,则该几何体的表面积是( )
某几何体的三视图如图所示,其中正视图和俯视图都是腰长为2的等腰三角形,俯视图是半径为1的圆,则该几何体的表面积是( )| A. | π | B. | 2π | C. | 3π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<-2,或a>0 | B. | 0<a<1 | C. | 1<a<3 | D. | 2<a<6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
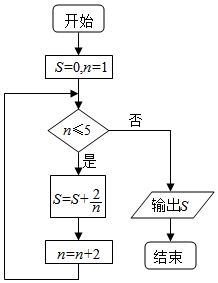
| A. | 2.$\stackrel{•}{6}$ | B. | 3.0$\stackrel{•}{6}$ | C. | 4.1$\stackrel{•}{6}$ | D. | 4.5$\stackrel{•}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
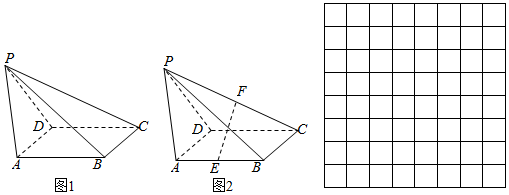
 如图,在棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为直角梯形,其中AB∥CD,AB⊥AD,AB=AC=2CD=4,AA1=3,过AC的平面分别与A1B1,B1C1交于E1,F1,且E1为A1B1的中点.
如图,在棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为直角梯形,其中AB∥CD,AB⊥AD,AB=AC=2CD=4,AA1=3,过AC的平面分别与A1B1,B1C1交于E1,F1,且E1为A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
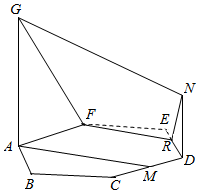 如图,已知ABCDEF是正六边形,GA、ND都垂直于平面ABCDEF,平面FGN交线段DE于点R,点M是CD的中点,AB=DN=1,AG=2.
如图,已知ABCDEF是正六边形,GA、ND都垂直于平面ABCDEF,平面FGN交线段DE于点R,点M是CD的中点,AB=DN=1,AG=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com