
分析 (1)由条件利用诱导公式、两角和的正弦公式,化简所给式子的值,可得结果.
(2)利用诱导公式化简所给式子的值,可得结果.
解答 解:(1)sin(-1320°)cos1110°+cos(-1020°)sin750°
=sin(4×360°-1320°)cos(1110°-3×360°)+cos(3×360°-1020°)sin(750°-2×360°)
=sin120°cos30°+cos60°sin30°=sin60°cos30°+cos60°sin30°=sin(60°+30°)=1.
(2)$\frac{si{n}^{2}(α-2π)cos(3π+α)}{cos(\frac{3π}{2}-α)cos(α-π)sin(-α-3π)}$=$\frac{{sin}^{2}α•(-cosα)}{-sinα•(-cosα)•sinα}$=-1.
点评 本题主要考查应用诱导公式、两角和的正弦公式化简三角函数式,属于基础题.


科目:高中数学 来源: 题型:选择题
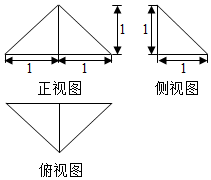
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
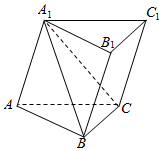 如图,三棱柱ABC-A1B1C1的体积为V1,四棱锥A1-BCC1B1的体积为V2,则$\frac{V_1}{V_2}$=$\frac{3}{2}$.
如图,三棱柱ABC-A1B1C1的体积为V1,四棱锥A1-BCC1B1的体积为V2,则$\frac{V_1}{V_2}$=$\frac{3}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,点P是半径为1的半圆弧$\widehat{AB}$上一点,若AP长度为x,则直线AP与半圆弧$\widehat{AB}$所围成的面积S关于x的函数图象为( )
如图,点P是半径为1的半圆弧$\widehat{AB}$上一点,若AP长度为x,则直线AP与半圆弧$\widehat{AB}$所围成的面积S关于x的函数图象为( )| A. | 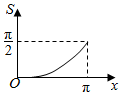 | B. | 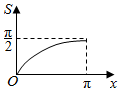 | C. | 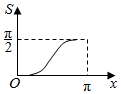 | D. | 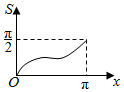 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4(4$\sqrt{2}$-$\sqrt{31}$) | B. | 4(4$\sqrt{2}$-$\sqrt{30}$) | C. | 4($\sqrt{33}$-4$\sqrt{2}$) | D. | 4($\sqrt{33}$-$\sqrt{31}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3f(ln2)>2f(ln3) | B. | 3f(ln2)=2f(ln3) | ||
| C. | 3f(ln2)<2f(ln3) | D. | 3f(ln2)与2f(ln3)的大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com