
分析 (1)利用绝对值不等式的性质得出f(x)的最小值;
(2)把1=$\frac{1}{2}$(a+b)代入左侧,利用基本不等式得出结论.
解答 解:(1)f(x)=|x-2|+|x-4|≥|(x-2)-(x-4)|=2,当且仅当2≤x≤4时等号成立,
∴m=2.
(2)证明:∵a+b=2,∴$\frac{1}{2}$(a+b)=1,
∴$\frac{1}{a}+\frac{1}{b}$=$\frac{a+b}{2a}+\frac{a+b}{2b}$=1+$\frac{b}{2a}$+$\frac{a}{2b}$=1+$\frac{1}{2}$($\frac{b}{a}$+$\frac{a}{b}$)≥1+$\frac{1}{2}$×2=2.
当且仅当$\frac{b}{a}=\frac{a}{b}$即a=b=1时等号成立.
点评 本题考查了绝对值不等式的性质,基本不等式的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
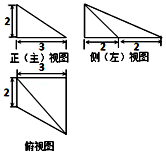
| A. | $2\sqrt{5}$ | B. | $4\sqrt{2}$ | C. | $\sqrt{29}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
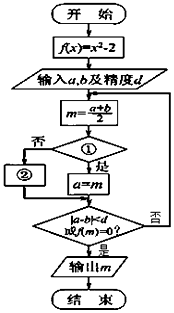
| A. | f(a)•f(m)<0?;b=m | B. | f(b)•f(m)<0?;b=m | C. | f(a)•f(m)<0?;m=b | D. | f(b)•f(m)<0?;b=m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com