
分析 用列举法确定基本事件的情况,由对立事件的概率计算公式得答案.
解答 解:令红球、黑球、白球分别为A,B,a,b,1,则从袋中任取两球有(A,B),(A,a),(A,b),(A,1),(B,a),(B,b),(B,1),(a,b),(a,1),(b,1),共10种取法,其中两球颜色相同有(a,b),(A,B),共2种取法,由古典概型及对立事件的概率公式可得P=1-$\frac{2}{10}$=$\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 本题考查了古典概型及其概率计算公式,考查了互斥事件和对立事件的概率计算公式,解答的关键是列举时做到不重不漏,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
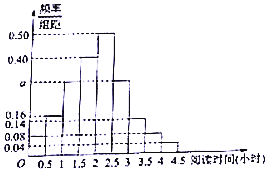 某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成样本的频率分布直方图如图所示.
某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成样本的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
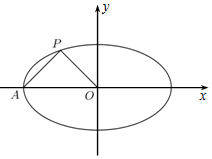 设椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A、中心为O,若椭圆M过点$P(-\frac{1}{2},\frac{1}{2})$,且AP⊥PO.
设椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A、中心为O,若椭圆M过点$P(-\frac{1}{2},\frac{1}{2})$,且AP⊥PO.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com